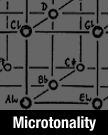
Theory

31-tone music: a unique experience

What is 31-tone music?

On hearing 31-tone music for the first time, you will not believe your ears. And you are right, the music is indeed different. The thrill of a first encounter will soon give way to attempts t o pinpoint the difference. At first you may think that this music lacks distinctness, next you may be struck by its subtleness, its refinement, its delicacy perhaps and the fact that it is definitely more colorful. You seem to hear more tones.

And you are right. Theoretically an octave can be divided into any number of tonal steps. The division of the octave into 12 steps of equal distance – introduced in the second half of the seventeenth century – has since become the tonal system for almost all music written in Western culture.

Almost all music, we said, and almost indeed, as for some time now music is being written and performed in a 31-tone temperament. It is music that aspires to produce more than a short-lived shock effect that could be comparable to the brilliant flaring up to a comet. It is music that means to remove some of the drawbacks inherent in the 12-tone temperament.

A short historical account

The 31-tone temperament is a formula; the 12-tone temperament, so familiar to us, is another one of these formulas. Being an intelligent simplification, the 12-tone temperament does sacrifice something, such as purity of intonation. In order to produce a pure third, for example, one must differentiate between a d-sharp and an e-flat. A d-sharp in order to sound a pure third in consonance with the b below and e-flat in order to produce a pure third from g down. The same thing applies to g-sharp an a-flat. The so-called mean-tone temperament, widely practiced until the advent of the 12-tone temperament, featuring an e-flat, but no d-sharps; in fact the mean-tone system made provision for a limited number of pure thirds. The advent of the 12-tone temperament caused a complete break: music conceived and written in a mean-tone temperament could no longer be performed in mean-tone, pure intervals. When we compare the mean-tone temperament with the 31-tone system, we find that all tones in the mean-tone scale happen to be represented in the 31-tone scale. This means that old music written in the mean-tone mode, can be restored ti its original speldour on a 31-tone instrument. The past is no longer inaccessible.

True renewal

The past is no longer a closed book to us. The 31-tone temperament makes it possible for music, written in the mean-tone mode, to be performed adequately and authentically today; the break with the past no longer exists and we will be able to delve further into that past since we have created new means to do just that. However, this is only one, be it curious and spectacular, effect of the advent of 31-tone music.

Of even greater importance, perhaps, is the opportunity it offers to open up new perspectives to the future of music. Is it a sign of times that we need something else and something different to add to our musical terms of reference? And could the advent of electronic music be explained as an attempt to get away from the limitations imposed by the classical tradition?
If that is the case, the 31-tone temperament offers an inspiring alternative, for it has more to offer, holds more promises, takes us back to the summit of pure intonations and pure intervals and it represents the Tabula Rasa, the clean slate, for the human mind to start afresh. The origins of 31-tone music are entirely a Dutch affair.
It was the great the great 17th century physicists and mathematician Christiaan Huygens (1629-1695) who – with the aid of logarithms invented in the same century – managed to devise a “new 31-tone harmonic cycle” as the purest subdivision of the octave. Professor A.D. Fokker (1887-1972), a fellow-countryman of Huygens’, is to be commended for putting Huygens’ views into practice with the help of modern-day technology. He masterminded the building of the 31-tone pipe organ in the Teylers Museum in Haarlem, Holland, back in 1950.
Since then the so-called “Archiphone” – an electronic musical instrument - was built on the basis of Professor Fokker’s ideas. Subsequently a number of forward-looking musicians shifted the emphasis from theory to practice. And that’s how a bright idea resulted in a truly new kind of fascinating music.
And it ‘s no longer a strictly Dutch matter. In America, too, a number of 31-tone instruments have been built. And the list of composers who have written in the 31-tone idiom includes many nationalities: Henk Badings, Anton the Beer, Jan van Dijk, Hans Kox (The Netherlands), Joel Mandelbaum (United States), Oedoen Partos (Israel), Ivan Wyschnegradsky (France), Eugen Frischknecht (Switzerland), Alan Ridout (Great Britain) and Aloys Hába (Czech Republic).

(text: Marinus Schroevers)

The 31-tone scale

	12-tone	31-tone
scale	scale12.mid	scale31.mid
dominant seventh chord	vierkl12.mid	vierkl31.mid

For an introduction to the 31-tone system, see the article Paul Rapoport: About 31-tone equal temperament.

For the background of the 31-tone system, see the article Adriaan Fokker: Equal Temperament and the Thirty-one-keyed Organ.