Les tempéraments égaux
A.D. Fokker: Les mathématiques et la musique. Trois conférences, chap. IV,
Archives du Musée Teyler vol. 10, Martinus Nijhoff, Den Haag, 1947.
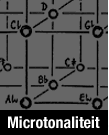
1. L'ensemble des sons, qui ont entre eux des rapports harmoniques, a été
rangé dans un réseau harmonique, selon le rapport de la quinte (suivant l'axe
des X), selon le rapport de la tierce majeure (suivant l'axe des Y) et selon le
rapport de la septième harmonique (axe des Z). Ces notes sont innombrables. Au
moyen de la voix, et d'un violon à touche unie qui permet un changement continu
de la hauteur du son, nous pouvons faire l'intonation juste d'un nombre quasi
infini de notes, mais il n'en est pas ainsi pour les instruments ou la touche
est divisée en cases par des sillets, ou pour les instruments à touches fixes,
comme l'orgue etc, ou pour les instruments à vent qui ont des trous fixes. Ces
instruments ne peuvent produire qu'un nombre limité de sons. D'autrepart, il y
a une limite à la faculté de distinguer les hauteurs des sons, et à la
précision avec laquelle on peut les entonner. Bref il sera nécessaire de se
restreindre et de n'utiliser qu'un nombre limité de sons différents.
2. Prenons le tableau des quintes et des tierces. Supposez que
| ut | o | o | o | o | o
| | pré | la | . | . | . | × | ×
| | fa | . | . | ré | × | ×
| | ré | la
| mi | si | fap | ×
|
vous ayez de la peine à faire la distinction d'un demi-ton majeur (15 : 16) et
d'un demi-ton mineur (24 : 25), ou bien que vous jugiez qu'il ne vaut pas la
peine de distinguer l'intervalle ut : ré de
ré : ré de
ré : ré. Cela revient à annuler
la différence de ut : ré. Cela revient à annuler
la différence de ut et ré et ré . On remplacera
alors, dans le tableau tous ses tons en ligne avec ut . On remplacera
alors, dans le tableau tous ses tons en ligne avec ut par les sons en
ligne avec ré par les sons en
ligne avec ré . A plus forte raison,
l'on identifiera le fa avec l'autre fap, qui n'en diffère
que d'un comma (80 : 81). Pour la même raison on identifiera tous les sons en
colonne avec fap avec leurs synonymes de la colonne de fa. Il ne reste donc que
douze sons distincts. . A plus forte raison,
l'on identifiera le fa avec l'autre fap, qui n'en diffère
que d'un comma (80 : 81). Pour la même raison on identifiera tous les sons en
colonne avec fap avec leurs synonymes de la colonne de fa. Il ne reste donc que
douze sons distincts.
Si l'on trace dans le tableau une droite contenant deux sons, il faut que cette
droite en contienne un nombre illimité, répétant toujours le même intervalle.
Par suite de nos identifications, nous retrouverons le même son après douze
intervalles au plus (peut-être après six, quatre, trois, ou deux intervalles).
Cela veut dire que douze de ces intervalles vaudront un nombre entier
d'octaves. Il en résulte que les douze sons auxquels nous nous bornons sont
répartis dans 1'octave à intervalles égaux. Nous avons défini le tempéramént
égal à douze demi-tons.
3. Plus tard, quand vous aurez acquis l'oreille plus fine, vous
refuserez à prendre un ut pour un ré pour un ré . Vous
remarquerez une différence, et vous penserez qu'en diézant le ut . Vous
remarquerez une différence, et vous penserez qu'en diézant le ut vous arrivez au ré vous arrivez au ré . Peut-être sera-ce exagérer un
peu la différence ré . Peut-être sera-ce exagérer un
peu la différence ré : ut : ut , comme il arrive
après les découvertes
nouvelles. Dans le tableau harmonique on peut rayer tous les sons en ligne avec
ut , comme il arrive
après les découvertes
nouvelles. Dans le tableau harmonique on peut rayer tous les sons en ligne avec
ut  , qui seront identifiés à d'autres. De même
seront rejetés comme doubles les sons qui ne diffèrent que d'un comma. , qui seront identifiés à d'autres. De même
seront rejetés comme doubles les sons qui ne diffèrent que d'un comma.
ut  | o | o | o | o
| | × | mi | . | . | ré
| | × | ut | . | . | . | ×
| | × | la | . | . | . | ×
| | × | fa | . | . | . | ×
| | ré | la | mi
| ri | ×
| | | | | | ré p p
|
On peut compter le nombre des sons indépendants dans
le tableau. Il y en en dix-neuf, et il couvre l'étendue d'un parallélogramme
ayant ses sommets aux points où se trouvent les ré .
Pour les mêmes raisons que nous avons données au paragraphe précédent, nous
répartirons ces sons en un tempérament égal, qui sera le tempérament de
dix-neuf tritotons à l'octave. .
Pour les mêmes raisons que nous avons données au paragraphe précédent, nous
répartirons ces sons en un tempérament égal, qui sera le tempérament de
dix-neuf tritotons à l'octave.
4. On peut suivre la mème voie si l'on se sert du réseau harmonique à trois
dimensions. Persistons dans l'identification de deux tons différant d'un comma.
D'un point arbitraire du résèau, d'un son quelconque, on tracera une arête au
point où se trouve le second son, qui sera considéré comme homophonique. Ce
sera un vecteur d'homophonie. Les coordonnées de ce point seront quatre
quintes, et une sous-tierce, c'est-à-dire (4, -1, 0).
Plus subtile encore est
la différence entre les deux demi-tons majeurs 15 : 16 et 14 : 15, ou, ce qui
revient au même, la distinction de 224 et 225. Alors on identifiera 224 et
225, 25.7 et 32.52, et on tracera dans le
réseau un second vecteur d'homophonie, de l'origine au point qui diffère de
deux quintes, de deux tierces, et d'une sous-septième; de coordonnées (2, 2,
-1).
En dernier lieu on remarquera que trois septièmes suivies d'une quinte nous
portent à un son presque identique au son de départ (3 × 7 × 7
× 7 = 1029, 210 = 1024. Nous identifierons ces deux sons. Dans
le réseau harmonique cette paire de sóns nous fournit un troisième vecteur
d'homophonie, aux coordonnées (1, 0, 3).
Ces trois vecteurs nous définissent dans le réseau un parallélépipède, une base
de périodicité. Seuls les notes intérieures à ce parallélépipède seront
indépendantes.
Leur nombre est défini par son volume, qui, par les méthodes de la géométrie
analytique, se trouve à l'aide du déterminant formé avec les coordonnées des
arêtes:
| 4 -1 0 |
| 2 2 -1 | = 31
| 1 0 3 |
Cette méthode nous fournit le tempérament égal de trente-et-un cinquièmes de
ton, tel qu'il a été calculé par Christiaan Huygens.
5. Mais de quoi s'agit-il au fond? Ne faisons-nous pas la musique
avec quelques intervalles fondamentaux: l'octave (2 : 1), la quinte (3 : 2), la
tierce majeure (5 : 4), et la'septième harmonique (7 : 4)? En disant que nous
les additionnons ou soustrayons, nous multiplions les fractions
correspondantes et ce que nous additionnons et soustrayons en vérité, ce sont
les logarithmes de ces fractions. Voici les lógarithmes approximatifs
| de l'octave . . . . . . . . | O = log 2 | = 0, 301 030 00 ...
| | de la septième . . . . . . . | S = log 7/4 | = 0, 243 038 05 ...
| | de la quinte . . . . . . . . | Q = log 3/2 | = 0, 176 091 25 ...
| | de la tierce . . . . . . . . | T = log 5/4 | = 0, 096 910 01 ... |
Nous avons affaire à quatre nombres irrationnels. Nous désirons
reproduire sur nos instruments les intervalles comme multiples d'un intervalle
élémentaire, qui se trouvera entre toutes les paires de touches voisines. C'est
à dire que nous désirons connaître un diviseur commun de ces intervalles. Or,
les logarithmes, en tant que nombres irrationnels, n'ont point de diviseur
commun. Cela est impossible. Il faut donc se contenter d'une appróximation
plus ou moins passable.
Voici le procédé: Le plus petit des nombres, T, sera soustrait des autres
autant de fois que possible, afin de laisser des restes aussi petits que
possible, fussent-ils négatifs. Après quoi, ce sont ces restes qu'il s'agira de
représenter le mieux possible par des multiples d'un diviseur commun. On
obtient ainsi:
| O = 3T + | R1, oú | R1 | = 0,0103 | = 1 | × 0,0103
| | S = 3T + | R2, | R2 | = -0,0477 | = -5 | × 0,0095
| | Q = 2T + | R3, | R3 | = -0,0177 | = -2 | × 0,0088
| | T = | R4, | R4 | = 0,0969 | = 10 | × 0,0097.
|
Par ce calcul rapide nous trouvons que les restes se prêtent à une
approximation de 1, -5, -2, 10 fois un diviseur à peu près constant. A l'aide
de ces nombres, nous trouvons un tempérament où les intervalles seront
approximativement définis par les nombres
O : S : Q : T (=) 31 : 25 : 18 : 10.
Nous retrouvons le tempérament de Huygens avec trente-et-un cinquièmes de
tons dans l'octave.
Cette méthode est empirique. Les mathématiques peuvent fournir une méthode
dirécte pour trouver des approximations en nombres entiers du rapport de
deux nombres irrationnels. Le problème de trois, ou même de quatre
nombres irrationnéls à la fois dépasse de loin les forces des mathématiciens
d'aujourd'hui.
6. En 1875, des études importantes ont été consacrées au problème du
tempérament égal par R.H.M. Bosanquet. Je veux suivre une de ses idées. En
procédant par quintes on arrive, de l'ut, par sol : ré :
la : mi au si. M. Bosanquet met f pour l'intervalle
si : ut.
Deux pas plus loin on arrive, si : fa à l'ut
à l'ut . M. Bosanquet met s pour l'intervalle ut :
ut . M. Bosanquet met s pour l'intervalle ut :
ut . On vérifie que
l'octave ut : ré : mi : fa : sol : la
: si : ut comporte cinq secondes majeures et deux secondes
mineures, appelées f. Une seconde majeure, de si à l'ut . On vérifie que
l'octave ut : ré : mi : fa : sol : la
: si : ut comporte cinq secondes majeures et deux secondes
mineures, appelées f. Une seconde majeure, de si à l'ut comprend
deux intervalles f + s. Donc, l'octavè est représentée par comprend
deux intervalles f + s. Donc, l'octavè est représentée par
O = 5 s + 7 f.
On peut ajouter les formules pour la quinte: Q = 3 s + 4 f, et pour la tierce
majeure: T = 2 s + 2 f.
Or, il y a deux styles, le style des anciens et celui des classiques après la
Renaissance.
Dans le tempérament des anciens, on a f = 256 : 243 et s = 2187 : 2048, de
sorte que s est supérieur à f.
Dans le tempérament des classiques, on
trouve f = 16 : 15 et s = 25 : 24, de sorte qu'ici c'est f qui l'emporte sur
s.
Dès qu'on ne veut plus posser f = s, il faut mettre cette différence en
évidence. Tout comme Huygens, Bosanquet remarque qu'on pourrait tenter de
choisir la différence des deux comme unité élémentaire du tempérament.
Suivant les anciens, prenant s > f, on pourrait poser
| s=2, f=1; | O=17, | Q=10, | T=6
| | s=3, f=2; | O=29, | Q=17, | T=10
| | s=4, f=3; | O=41, | Q=24, | T=14
| | s=5, f=4; | O=53, | Q=31, | T=18 |
On pourrait prolonger cette liste.
D'autre part, suivant les classiques, avec s < f, on posera
| s=1, f=2; | O=19, | Q=11, | T=6
| | s=2, f=3; | O=31, | Q=18, | T=10
| | s=3, f=4; | O=43, | Q=25, | T=14 |
et ainsi de suite.
On pourrait aussi choisir la moitié de la différence entre s et f comme unité
élémentaire du tempérament. Dans le style ancien la fixatión s=3, f=1
entraînerait O=22; et s=5, f=3 nous donnerait O=46. Dans le style
classique; on aurait O=26 pour s=1, f=3, et O=50 pour s=3, f=5.
Voilà une foule de possibilités, provenant de ce raisonnement de Bosanquet, et
il y en a d'avantage. Bien entendu, il nous faut une mesure pour choisir le meilleur
tempérament!
7. En effet, il est possible de formuler un critérium pour l'efficacité de
l'approximation aux exigences idéales.
On prendra les nombres irrationnels qui
représentent les intervalles justes fondamentaux, et l'on mettra en évidence
leurs proportions mutuelles en construisant un bloc rectangulaire ayant pour
arétes ces nombres irrationnels. La diagonale de ce bloc indiquera fidèlement
leurs rapports par sa direction.
Lorsqu'on prend des nombres entiers qui devront réaliser une approximation aux rapports idéaux,
on pourra construire un bloc rectangulaire ayant sés arêtes proportionnelles à ces nombres entiers.
On aura une nouvelle diagonale. Tant que la direction de cette diagonale déviera
de la diagonale qui représente les nombres idéaux, l'approximation sera
défectueuse. La déviation des deux directions doit être comprise commé la
différence entre deux rayons vecteurs unitaires menés suivant les deux directions.
Telle sera notre mesure d'efficacité. Rien n'empêche de l'appliquer
au cas de quatre nombres, en construisant un bloc à quatre dimensions.
Il faut commencer par construire le rayon vecteur unitaire correspondant aux
nombres exacts.
Les composantes de ce rayon vecteur sont définies par
O = 0,690 455
S = 0,557 442
Q = 0,403 890
T = 0,222 277
Dans le tempérament à douze demi-tons on pose
O12 : S12 : Q12 : T12 = 12 : 10 : 7 : 4.
Le rayon vecteur représentant ce tempérament a les composantes
O12 = 0,682 66
S12 = 0,568 88
Q12 = 0,398 22
T12 = 0,227 55
Le calcul du carré de la déviation donne d2 = 0,000 252.
Prenons ensuite le tempérament à trente-et-un cinquièmes de ton, où
O31 : S31 : Q31 : T31 = 31 : 25 : 18 : 10.
Le rayon vecteur représentant ce tempérament a les composantes
O31 = 0,691 455
S31 = 0,557 625
Q31 = 0,401 490
T31 = 0,223 050
Le carré de la déviation se réduit à d2 = 0,000 007 38.
Pour terminer, le tempérament à cinquante-trois commas,
O53 : S53 : Q53 : T53 = 53 : 43 : 31 : 17
est représenté par un rayon vecteur de composantes
O53 = 0,689 534
S53 = 0,559 433
Q53 = 0,403 332
T53 = 0,221 171
On trouve pour le carré de la déviation d2 = 0,000 006 38.
Il est curieux de remarquer que l'augmentation considérable du nombre de 31 à
53 n'entraîne qu'une amélioration médiocre.
8. L'étude des composantes de ces rayons vecteurs représentant tempéraments
mène à une conclusion assez évidente, bien qu'in attendue. On remarquera, par exemple
dans le temperament des trente et un cinquièmes de ton, que
O31 > O; S31 > S; T31 > T, tandisque Q31 < Q.
On s'est accoutumé à l'exigence que l'octave soit accordée dans sa juste
mesure, et que les unités élémentaires soient une partie aliquote de l'octave
juste. Cette exigence est-elle bien fondée? Pourquoi cette exemption de
l'octave des fautes et des offenses du tempérament? Je n'y vois point de
raison. D'ailleurs, il est bien rare de trouver un piano qui ait les octaves
justes.
Pour rendre justice égale aux intervalles fondamentaux et au tempérament, il
importe de dilater l'octave de O = 0,690 455 en O31 = 0,691 455,
savoir 1 sur 690, d'accorder la septième sensiblement juste, puisque S = 0,557
422 et S31 = 0,557 625 sont presque égaux, de comprimer la quinte
Q = 0,403 890 en Q31 =
0,401 490, en la diminuant de 2,4 pour 400, ou bien 1 pour 167, et de dilater
la tierce majeure de T = 0,222 277 en T31 = 0,223 050, d'une
dilatation de 1 pour 300.
La trente-et-unième partie aliquote de l'octave juste correspond à un rapport de
fréquences 1,022 612. La trente-et-unième partie aliquote de l'octave tempéré
corréspond à un rapport de fréquences 1,022 645. Deux de ces unités
élémentaires font approximativement
2 45 2 × 45 + 1 2 45 3 × 45 + 1
(1,022 612) = -- × ----------; (1,022 645) = -- × ----------
44 2 × 44 + 1 44 3 × 44 + 1
Le deuxième facteur est toujours très légerement infériéur au premier.
Avant de conclure, il faut signaler que, au lieu de préndre la quinte, on
pourrait choisir la quarte comme intervalle fondamental. Suivant la même
méthode, on serait conduit à une légère contraction de l'octave dans le
tempérament égal. Une contraction permettrait d'ailleurs la réalisation d'une
condition musicale, formulée par Robert Smith (XVII siècle). Il exigeait la
méme fréquence des battements pour les quintes et les sixtes majeures. Il est
trop tard maintenant pour approfondir cette question.
A. D. Fokker, 1947
Littérature
- Leonhard Euler, Tentamen novae theoviae musicae, Petropoli, 1739,
Opera Omnia, series III, volume I, p. 252.
- Giuseppe Tartini, Trattato di Musica, Padova, 1754.
- Mart. J. Lürsen, Grondslagen van de muziektheorie, Den Haag, 1944.
- Mart. J. Lürsen, Modi antiche, musiche nuove, Haarlem, 1947.
- Ernst Krenek, Über neue Musik, Wien, 1937.
- R.H.M. Bosanquet, The theory of the division of the octave, and the practical
treatment of the musical systems thus obtained, Proc. Roy. Soc. London XXIII, 390, 1875.
- A.D. Fokker, Rekenkundige bespiegeling der muziek, Gorinchem, 1945.
|