
Below is a reproduction of chapter 80 from the book Singen ist das Fundament zur Music in allen Dingen which is a collection of documents about Telemann. It is a revised version of the paper "Neuen Musikalischen Systems" that Telemann had sent in 1742 or 1743 to the Societät der musikalischen Wissenschaften founded by Lorenz Christoph Mizler. At the age of 86 Telemann was still engaged to pave new roads for music, and increase the knowledge about the theory of intervals.

So after all it wasn't the Kapellmeister's last occupation and he had done some
other labour after writing this article.
Page 267:

Page 268:

Page 269:

Page 270:

Page 271:

Page 272:

Page 273:

Telemann divides the chromatic semitone into four commas, and the whole tone in
nine commas. He explains that sharps and flats are not the same and that sharps
are lower: C (ces) is lower than D
(ces) is lower than D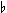 (déb).
He doesn't say which comma he means, the syntonic or Pythagorean comma. This
doesn't matter much since they are almost the same, and at that time the
distinction was often not made. So ces is four commas higher than C and cex four
commas higher than ces, etc. On page 272 he states that the whole tones stride
in equal pace, so they are all 9 commas wide. What he doesn't specify
unfortunately is the size of the diatonic semitone (distance of E to F and B to
C). Is it equal in size to the chromatic semitone, 4 commas or a comma larger,
5 commas?
(déb).
He doesn't say which comma he means, the syntonic or Pythagorean comma. This
doesn't matter much since they are almost the same, and at that time the
distinction was often not made. So ces is four commas higher than C and cex four
commas higher than ces, etc. On page 272 he states that the whole tones stride
in equal pace, so they are all 9 commas wide. What he doesn't specify
unfortunately is the size of the diatonic semitone (distance of E to F and B to
C). Is it equal in size to the chromatic semitone, 4 commas or a comma larger,
5 commas?
The former possibility leads to a system comparable to 53-tone equal
temperament in that the tones of his system form a subset of 53-tET or
something close to it. In 53-tET, there are 9 steps in the whole tone and 4 in
the diatonic semitone: 5×9+2×4=53 and the fifth is virtually
pure.
Georg Andreas Sorge interpreted Telemann's description as a tone set in 55-tone
equal temperament. The fifth in 55-tET, 698.182 cents, is very close to the
1/6-comma tempered (meantone) fifth: 698.371 cents. Having 9 steps for the
whole tone and 5 for the diatonic semitone, one gets a total of
5×9+2×5=55. There are several reasons why the latter possibility,
55-tET, is the most probable.
The fact that C is lower than D
is lower than D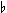 implies that
the fifth is tempered (made flat by a small amount). A counterargument might be
that Telemann says nowhere in the article that the fifth should be tempered, he
even makes an allusion to the temperament wars for the keyboard which don't
apply to unfretted instruments like the violin!
implies that
the fifth is tempered (made flat by a small amount). A counterargument might be
that Telemann says nowhere in the article that the fifth should be tempered, he
even makes an allusion to the temperament wars for the keyboard which don't
apply to unfretted instruments like the violin!
At the bottom of page 268 he says that E-F and B-C are a "small tone"
(kleinen Ton), which probably means nothing more than to say it's a
semitone. The same term however is used for the distance C-Db (bottom of page
269), which is 5 commas and not 4. He might have used the words "small
semitone" or "large semitone" which words he uses at the bottom of page 271, if
he wanted to say which of those the diatonic semitone was meant to be.
Curiously however, he has an objection against the succession of small and
large semitones, says they limp with a short and a long foot from C until the
major third. He seems to contradict himself because unequal semitones are a
direct result of the odd number of commas, 9, in the whole tone.

There is a problem with 53-tET when it's used for Telemann's music and music of
his time, which is the comma problem. The syntonic comma is an audible distance
in 53-tET; going upwards by four fifths and down by two octaves gives a major
third that sounds out of tune. Therefore some chords can't be made to sound in
tune, like this one:
The only way is to temper the fifth by a small amount.
In 55-tET, the major second E-F is the same distance as C-D,
but in 53-tET it is not: one comma smaller. On page 270 the major third is
shown as D-F
is the same distance as C-D,
but in 53-tET it is not: one comma smaller. On page 270 the major third is
shown as D-F and the minor third as D-F. If E-F had been 4
commas instead of 5, it would be a very flat minor third.
and the minor third as D-F. If E-F had been 4
commas instead of 5, it would be a very flat minor third.
In a letter to Carl Heinrich Graun from 15 December 1751, page 248 in the book,
he writes that D -F
-F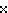 is a major third and
D
is a major third and
D -G a diminished fourth (or "smallest fourth" in his
terminology) and implies that these intervals have a different size; this
is also consistent with 55-tET.
-G a diminished fourth (or "smallest fourth" in his
terminology) and implies that these intervals have a different size; this
is also consistent with 55-tET.
The habit with keyboard instruments was to tune the major third larger than
pure. In 53-tET there are two major thirds, one is smaller than pure and the
other is very large, close to the untempered Pythagorean third. The major third
in 55-tET is in between those.
So we can conclude that Telemann means the 4-comma chromatic semitone to be the
traditional semitone which is the difference between 7 tempered fifths and 4
octaves. This is inconsistent with 53-tET where the size is 5 commas.
The movement in the fourth paragraph on page 271 can be heard by a
MP3-file in 55-tET, made by Joe Monzo.
Other composers in his time advocated the use of a tempered fifth around 1/6- or 1/5-comma smaller than just, like Leopold Mozart in his violin method of 1756. In this method the student has to practice in distinguishing the large diatonic and the small chromatic semitones and playing flats a comma higher than enharmonically equivalent sharps, which Telemann demands here too.
The reason why Telemann designed his system is given in Sorge's title of 1748: Zu Beförderung reiner Harmonie entworffen (Designed to promote pure harmony). The basic intervals like the perfect fifth, major and minor third are approximated well in 55-tET, but they are not exactly just. So we should be cautious to consider Telemann's system as a rigid prescription of a 55-tone equal tempered basic scale. It was not designed to be a keyboard temperament but of course when a violin is accompanied by a tempered keyboard instrument it should temper accordingly for the sake of harmony. And in practice the variations in intonation by a violin will be larger than the comma fractions we are talking about here. Anyway the minor and major thirds are still better in 1/6-comma meantone than in 12-tone equal temperament. But note that no exact value for the tempered fifth is given by Telemann and our assumption that it's close to the 55-tET fifth is an indirect inference.
Looking at the table on page 267 we see 7×6+2=44 different names.
Telemann says nothing about any equivalences between the tones of his system.
Putting them in ascending order using the 55-tET step as the comma indeed gives
no enharmonic equivalences. All the tones belong to one long cycle of 43
tempered fifths, 22 from C in the downward direction and 21 in the upward
direction. Why not more tones? The reason he gives looks like a tautology: the
cause for not using double signs is, because then 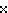
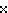 and ßß would originate.
and ßß would originate.
The first column is the total number of commas from c:
| 0: | c |
| 1: | debb |
| 3: | hax |
| 4: | ces |
| 5: | déb |
| 6: | ebbéb |
| 8: | cex |
| 9: | d |
| 10: | ebb |
| 11: | febbféb |
| 12: | cexces |
| 13: | des |
| 14: | éb |
| 15: | febb |
| 17: | dex |
| 18: | e |
| 19: | féb |
| 20: | gebbgéb |
| 22: | es |
| 23: | f |
| 24: | gebb |
| 26: | ex |
| 27: | fes |
| 28: | géb |
| 29: | abbáb |
| 31: | fex |
| 32: | g |
| 33: | abb |
| 35: | fexfes |
| 36: | ges |
| 37: | áb |
| 38: | habbháb |
| 40: | gex |
| 41: | a |
| 42: | habb |
| 43: | cebbcéb |
| 45: | as |
| 46: | háb |
| 47: | cebb |
| 49: | ax |
| 50: | h |
| 51: | céb |
| 52: | debbdéb |
| 54: | has |
| 55: | c' |
These names are a bit confusing for us being used to ces =
C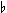 and not C
and not C .
Telemann says the names sound rather awkward but that might have been true
also when one heard the names cis, dis, fis, etc. for the first time.
.
Telemann says the names sound rather awkward but that might have been true
also when one heard the names cis, dis, fis, etc. for the first time.
Needless to say perhaps, this interval system wasn't designed to be a microtonal system. Some intervals he says are awful, but they are necessary to be known by those who deal with transposition.
Manuel Op de Coul, 2001.