Gioseffo Zarlino da Chioggia (c.1517-1590)

In de grote tijd van de ontwikkeling der polyphonie in de Nederlanden kwam Adriaen Willaert naar Italië. Gioseffo Zarlino was zijn opvolger als kapelmeester in Venetië. Het hoogtepunt van Zarlino's werken valt in het derde kwartaal van de zestiende eeuw. Zijn boeken verschenen tussen 1550 en 1590. Daarin heeft hij een grote codificatie gegeven van de regels, die na de opbloei van de genoemde polyphone kunst voor het contrapunt in gebruik gekomen waren.
Geschilderd portret van Zarlino, Bologna Zarlino legt daarbij de rechten vast van de harmonische grote terts. In Hugo Riemanns Geschichte der Musiktheorie vindt men beschreven, hoe deze vermoedelijk uit het noorden (Walter Odington) zijn weg gevonden heeft naar de landen om de Middellandse Zee. Bij de middeleeuwse schrijvers vindt men bijna steeds vermeld de sekunde van Pythagoras en de terts van Pythagoras, die de som van twee dergelijke sekunden is. In het zuiden brak reeds Bartholomeus Ramis de Pareia met de terts van Pythagoras. Bij Zarlino vindt men de definitieve aanvaarding van de harmonische grote terts (getalverhouding 4:5) als fundamentele faktor in de harmonie.

De harmonische beschouwingen van die tijd kleden zich meestal in de vorm van het probleem, hoe men een gespannen snaar moet verdelen om gewenste intervallen te krijgen. De eenvoudigste verdeling van de snaar is in tweeën. Het is bekend, dat de halve snaar een toon geeft, die met de lagere toon van de hele snaar een interval maakt, dat men een oktaaf is gaan noemen. Wat ligt er meer voor de hand, dan dat men het verschil tussen deze twee snaarlengten opnieuw in tweeën gaat verdelen? Indien het een D-snaar is, zal men met de halve snaar krijgen d, en met driekwart van de snaar een G. Op een bepaalde manier mag G het midden heten tussen D en d. Daar de driekwart snaarlengte het rekenkundig of arithmetisch gemiddelde is van l en 1/2, noemde men G het arithmetische midden van het oktaaf D : d. Zeer voor de hand ligt het ook, dat men het verschil tussen de hele en de halve snaarlengte in drieën deelt. Dat betekent dat men luistert naar welke tonen gespeeld worden met 1/2, of 3/6, met 4/6 (of 2/3), met 5/6 en met de hele snaarlengte. Door die tonen wordt het oktaaf arithmetisch in drieën gedeeld. Op de D-snaar zijn het d : A : F : D. Het zal duidelijk zijn, dat men nu tussen F en d de toon A het arithmetische midden is, en dat tussen de tonen D en A de toon F het arithmetische midden is. In wat tegenwoordig heet de kleine-tertsdrieklank D : F : A is dus F het arithmetische midden van de kwint D : A. Op deze wijze kan de primitieve mens doorgaan. Bijvoorbeeld kan hij het stuk op de snaar tussen de helft (d) en tweederde (A) in drieën delen. Dan krijgt hij de snaarlengten 9/18 (of 1/2), 10/18 (of 5/6), 11/18 en 12/18 (of 2/3). Wij kunnen dat in ons notenschrift en met onze letters nog niet goed weergeven, maar het is een tamelijk verbreide toonopvolging, waarbij de kwart d : A arithmetisch in drieën gedeeld is.
Een andere wijze van delen, die de harmonische verdeling genoemd wordt, vindt een voorbeeld in de oktaafverdeling D : A : d. De afstand, op de snaar gemeten, van D naar A, - dat is 1 - 2/3 = 1/3 snaarlengte, - staat in dezelfde verhouding tot de afstand van A naar d, - dat is 2/3 - 1/2 = 1/6 snaarlengte, - als de snaarlengte van D, dat is 1, tot de snaarlengte van d, dat is 1/2. Dit is minder primitief! Men vereenvoudigt echter de voorstelling, door aan de omgekeerden van de snaarlengten te denken. Dan beantwoordt aan D het omgekeerde van de snaarlengte 1/1 = 1, en aan d beantwoordt het omgekeerde van de snaarlengte 1/2, dat is 1 / (1/2) = 2, en het gemiddelde van deze 1 en 2 is 1 1/2, dat is het omgekeerde van 2/3, en 2/3 is de snaarlengte die aan A beantwoordt. A heet het harmonisch midden tussen D en d. Men kan nu het oktaaf harmonisch in drieën delen. Dan moet men de afstand van de "omgekeerde" 1 en 2 in drieën delen, dat geeft 1 = 3/3, 4/3, 5/3 en 6/3 = 2, en de corresponderende snaarlengten zijn 1, 3/4, 3/5, 1/2, die beantwoorden aan D : G : B : d. Hier is G het harmonische midden tussen D en B, en B het harmonische midden tussen G en d. In de grote-tertsdrieklank G : B : d is dus de kwint harmonisch middendoor gedeeld.
Tegenwoordig weten wij dat de harmonische verdeling betekent de gewone verdeling van het verschil in de trillingsgetallen, in de frequenties der intervaltonen. Verdeling van de verschillen in snaarlengten geeft de arithmetische verdeling van de kwint, de kleine-tertsharmonie. Verdeling van de verschillen in frequenties geeft de harmonische verdeling van de kwint, de grote-tertsharmonie.
Zarlino grondvest zijn harmonie op die twee drieklanken, dat is op de harmonische en op de arithmetische middendeling van de kwint. Behalve faktoren 2 zijn daar rekenkundig slechts faktoren 3 en 5 bij betrokken. Tot middendeling van de kwart gaat hij nog niet over. De arithmetische deling zou tussen de getallen 6 en 8, die zich verhouden als 3 en 4, een getal 7 geplaatst hebben. De harmonische zou, tussen de breuken 1/8 en 1/6, die zich verhouden als 3 en 4, een breuk 1/7 gezet hebben, en het getal 7 laat Zarlino in zijn harmonie niet toe.
Trouwens, in zijn tijd was het nog nodig te betogen, dat de harmonische grote terts, met de getalsverhouding 4:5, consonant was en niet dissonant, zoals men hem in de middeleeuwen had geacht te zijn. Daarover streed men toen. Zarlino heeft in zijn wetboek voor de harmonie ondubbelzinnig het goede recht van de harmonische tertsen vastgelegd. Verder ging Zarlino niet. In de grondslag waarop hij bouwt, wat het rekenkundige betreft, neemt hij geen andere getallen op dan 1, 2, 3, 4, 5, 6, de "senario", zoals die groep getallen in het Italiaans heet. Door de keuze van de harmonische terts komt Zarlino geheel vrij van de ban van het tetrachord van Pythagoras.

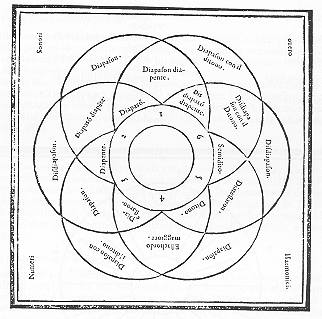
Diagram van het numero senario

Diagram waaruit blijkt dat alle mogelijke getalcombinaties binnen het numero senario consonanten opleveren.

In zijn Istitutioni Harmoniche van 1558 somt Zarlino de geslachten en de soorten van de oude tetrachorden op. Een tetrachord, dat betekent een groep van vier tonen, waarvan de uiterste zuiver een kwart van elkaar verwijderd zijn. De beide andere tonen kunnen dat interval op uiteenlopende wijze verdelen, en naar die verscheidenheid worden de geslachten geklassificeerd. Is er nergens tussen twee buren een interval groter dan een sekunde (hele toon) dan behoort het tetrachord tot het diatonische geslacht. Bedraagt het interval tussen de twee hoogste tonen anderhalve toon, dan heet het geslacht chromatisch. Bedraagt het interval van het hoogste paar tonen een grote terts, dan heet het geslacht enharmonisch. Deze namen zijn, met gewijzigde betekenis, nog in gebruik. Zarlino citeert Ptolemaeüs (in zijn spelling Tolomeo), en onderscheidt met hem vijf soorten in het diatonische geslacht. Diatonico diatono heet het tetrachord met twee sekunden van Pythagoras (9:8) en een limma van Pythagoras (256/243). Diatonico equale heet het tetrachord met de arithmetische verdeling in drieën, hierboven genoemd, dat nog voortleeft in de Schotse doedelzakmuziek. Diatonico sintono is de soort, waarin de hoogste en op één na laagste toon een harmonische grote terts vormen (frequentieverhouding 15:16:18:20). Twee van zulke tetrachorden naast elkaar gezet, met gemeenschappelijke grenstoon (B : c : d : e en e : f : g : a) maken de sinds Zarlino klassieke traditionele diatonische grote-tertstoonladder.
De andere soorten van het diatonische geslacht heeft Zarlino terzijde geschoven. Buiten de "senario", buiten de getallen één tot zes, was er voor hem geen harmonie. Het getal 11, in de genoemde toonsoort diatonico equale, past hem dus niet. Maar ook het getal 7, dat voorkomt in de frequentieverhoudingen van de nog niet genoemde toonsoorten diatonico molle (60:63:70:80) en diatonico toniaco (27:28:32:36) verwerpt Zarlino. Om dezelfde reden neemt hij ook niets over van de tetrachorden der chromatische geslachten, evenmin kan hij iets beginnen met de enharmonische toongeslachten.
Van een denkbeeld, of misschien in de kerktonen nog iets zou kunnen voortleven van die oude toongeslachten, vinden wij bij Zarlino niets. In zijn werk wordt onder al dat oude een streep getrokken, en een nieuw tijdperk begint met een polyphonie uitsluitend op de consonantie van harmonische kwint en terts gebaseerd, volgens de "monochordo diatonico sintono", onze traditionele grote-terts toonladder.

Op het stuk van de syntonische komma maakt Zarlino een belangwekkende ontwikkeling door. In de grote-tertstoonladder (op c) is de kwint tussen de tweede en de zesde trap (d : a) niet zuiver. Er ontbreekt een komma aan. Dat komt hiervandaan, dat vier zuivere kwinten een komma (81:80) groter zijn dan twee oktaven plus een harmonische grote terts. Ook is het interval tussen eerste en tweede trap (c : d) een sekunde van Pythagoras (8:9) terwijl dat tussen tweede en derde trap een kleine grote sekunde (9:10) is. Bij modulaties rijzen hieruit verschillende bezwaren, en de vraag is, hoe een redelijk compromis te vinden in een "temperamento" d.i. een voorschrift van stemming, volgens hetwelk men orgels en andere instrumenten met vaststaande toetsen kan stemmen.
In zijn Istitutioni van 1558 verdeelt Zarlino de komma in zeven delen. De kwinten stemt hij 2/7 komma te klein, de grote terts en de kleine terts elk 1/7 komma te klein, en zo verder. De sekunden worden aan elkaar gelijk gemaakt, en elk de helft van een grote terts.
Later, in 1571, doet Zarlino een andere oplossing aan de hand, die minder aan de kwinten tornt, en de grote terts volkomen zuiver laat. Voor de "Dimostrationi Harmoniche" heeft hij de gesprekvorm gekozen, afwisselende uiteenzettingen en discussies van hemzelf, sprekende met de kapelmeester Francesco Viola uit Ferrara, met Adriaen Willaert, zijn voorganger aan de signoriale kapel in Venetië, en met de Venetiaanse organist van de kerk San Marco, met Claudio Merulo. Dezen laat hij de noodzaak van een rationeel temperament betogen en Zarlino zelf komt dan met de oplossing te voorschijn, dat men de kwinten alle een kwart komma kleiner zal maken dan ze behoren te zijn. Dat is de zogenaamde middentoonstemming, waarbij de grote sekunde precies het midden treft van de zuivere harmonische terts. In deze stemming heeft men twee eeuwen sindsdien gemusiceerd.
Nog later, in 1588, wordt Zarlino geprest tot de bespreking van de normale halftoonstemming. In zijn "Sopplementi Musicali" polemiseert hij tegen een gewezen leerling, die hij overigens niet noemt, die de stelling verdedigde, dat de verkorting van een snaardeel tot 17/18 van de aanvankelijke lengte de toon zoveel hoger brengt, dat twaalf zulke stappen, alle even groot, samen een oktaaf maken, Zarlino rekent uit, welke verhouding men krijgt, indien men 18/17 twaalf maal met zichzelf vermenigvuldigt. Het is nog niet 2/1. Er ontbreekt 3/5 komma aan. Wij zouden zeggen, dat de benadering van 1/12 oktaaf door 18/17 dus zeer goed is (betere benadering is 17,8/16,8), maar Zarlino verwerpt ze. Van zijn kant geeft hij een meetkundige constructie voor de oktaafverdeling in twaalven op de snaar, en zelfs drie constructies. Dit zijn geen recht het doel rakende constructies met passer en lineaal, het zijn constructies van zo goed mogelijk proberen een lijn te trekken, die aan bepaalde eisen voldoet. Het valt te betwijfelen of de benadering, op deze wijze te bereiken, ooit beter kan zijn dan die door de breuk 18/17. De juiste getalverhoudingen voor de verdeling van het octaaf in twaalf gelijke parten, als tiendelige breuken met 4 decimalen, zijn in het begin der 17de eeuw berekend door Simon Stevin.
Voor instrumenten met vaste toetsen, orgels, luiten, enz. laat Zarlino de bruikbaarheid van deze normale halftoonstemming gelden, maar in een speciaal hoofdstuk betoogt hij uitdrukkelijk, dat wij in de zang uitsluitend de diatonisch syntonische toonsoort van Ptolemaeüs gebruiken, er dat bij meerstemmigheid de intervallen in hun zuivere verhoudingen gezongen worden. Anders dan Simon Stevin, die als grondstelling kiest, dat alle halftonen in hun volmaaktheid aan elkaar gelijk zijn, houdt Zarlino uitdrukkelijk vast aan de zuiverheid der consonanties.

In het tweede deel, caput 12, van de Istitutioni zet Zarlino op een merkwaardige manier tegenover elkaar de eigenlijke harmonie, en de niet-eigenlijke harmonie, Harmonia Propia en Harmonia Non propia. De eerste, zegt hij, heeft de macht om de ziel tot onderscheidene hartstochten bereid te maken en te bewegen, zij wordt geboren niet alleen door de consonanties, maar door de dissonanties evengoed, daarom leggen de goede musici zich erop toe, in de harmonieën de dissonanties met elkaar tot overeenstemming te brengen. De niet-eigenlijke harmonie kan beter harmonieuze consonantie heten, zegt Zarlino (hoor!), dan harmonie, ze bevat in zich geen enkele modulatie, ze heeft generlei macht om de ziel tot hartstocht te brengen, zoals de eigenlijk geheten harmonie dat heeft, die samengesteld is uit de vele niet-eigenlijke harmonieën.

Zarlino is een man van grote allure. Als beweegreden voor het schrijven van zijn Istitutioni Harmoniche zegt hij op de eerste bladzijden, dat de goddelijke muziek jammerlijk in verval geraakt is, zo dat een iegelijk zich permitteert ze te beschimpen en smadelijk te bejegenen. God in Zijn genade echter heeft een man als Adriaen Willaert doen geboren worden, een van de zeldzaamste intellecten, die ooit de muziek beoefenden, en die begonnen is de muziek op te heffen en ze te herstellen in die eer en waardigheid, die eertijds de hare waren. Met ditzelfde ideaal voor ogen stelt Zarlino zijn kennis en wetenschap te boek. Aan het eind van zijn werk schrijft Zarlino over de eisen, die gesteld mogen worden aan een musicus, die het in zijn vak tot enige volmaaktheid wil brengen. Hij moet welbedreven zijn inzake de rekenkunde en het omgaan met getallen en met breuken. Hij moet een uitstekend gehoor hebben. Hij moet bedreven zijn in de kunst van zingen, en van het contrapunt. Hij moet terdege thuis zijn in de klassieke literatuur, en in de geschiedenis en het karakter der volkeren. Hij moet een algemeen ontwikkeld mens zijn. Wij mogen ons ervan verzekerd houden, dat Zarlino zelf in hoge mate aan die standaard beantwoordde.
Deze schets wil ik besluiten met de spreuk, die in het Grieks op de titelbladen van zijn boeken prijkt:

Zolang God schenkt, vermag de nijd niets,
en indien Hij niet schenkt, baat ons zwoegen niemendal.

A.D. Fokker, 1945

Istitutioni harmoniche

De Istitutioni harmoniche (1558, 1589) zijn op het internet te lezen in de Thesaurus Musicarum Italicarum.

Stemming

Zarlino stelde dus, in navolging van Pythagoras, een methode van stemming vast door deling van een gespannen snaar op een monochord. Hij ging verder dan Pythagoras door de snaar ook in negen delen te verdelen, 4/9 en 5/9 levert de verhouding 4:5, de consonante grote terts; en elf delen, 5/11 en 6/11 levert 5:6, de consonante kleine terts. Uit de verhoudingen 1/1, 6/5, 5/4, 4/3, 3/2, en 2/1 werden de overige intervallen door berekening vastgesteld. Deze intervallen waren:
kleine secunde = reine kwart - reine grote terts = 4/3 : 5/4 = 16/15
grote grote secunde = 2 reine kwinten - octaaf = 3/2 × 3/2 : 2/1 = 9/8
kleine grote secunde = grote sext - reine kwint = 5/3 : 3/2 = 10/9
kleine sext = reine kwint + kleine secunde = 3/2 × 16/15 = 8/5
grote sext = reine kwart + grote terts = 4/3 × 5/4 = 5/3
kleine kleine septime = octaaf - grote grote secunde = 2/1 : 9/8 = 16/9
grote kleine septime = octaaf - kleine grote secunde = 2/1 : 10/9 = 9/5
grote septime = reine kwint + grote terts = 3/2 × 5/4 = 15/8
Zarlino's majeur toonschaal is

1/1   9/8    5/4     4/3   3/2    5/3   15/8     2/1
   9/8   10/9   16/15   9/8   10/9   9/8    16/15

En zijn mineur toonschaal

1/1   9/8    6/5     4/3   3/2    8/5    9/5     2/1
   9/8   16/15  10/9    9/8   16/15  9/8    10/9

Verder komen enkele oorspronkelijke intervallen ook in een andere verhouding voor:
kleine terts = reine kwart - grote grote secunde = 4/3 : 9/8 = 32/27
grote sext = octaaf - deze kleine terts = 2/1 : 32/27 = 27/16
kwart = kleine terts + grote grote secunde = 6/5 × 9/8 = 27/20
kwint = reine kwart + kleine grote secunde = 4/3 × 10/9 = 40/27
De overige chromatische intervallen zijn op een soortgelijke manier af te leiden. Omdat er twee hele toonsafstanden van 10/9 en 9/8 zijn, en maar een diatonische halve toonsafstand van 16/15, zijn er twee chromatische halve toonsafstanden, namelijk 9/8 : 16/15 = 135/128 en 10/9 : 16/15 = 25/24. De intervallen c-cis en des-d zijn 135/128, en de intervallen d-dis en es-e zijn 25/24. Tussen cis en des is het kleine verschil 2048/2025 (diaschisma geheten) en tussen dis en es 128/125 (kleine diëze).

Zie ook Olivier Bettens: Intonation juste à la Renaissance: idéal ou utopie?.

19-Toonsklavier

Het 19-toonsklavier dat Domenico Pesarese
in 1548 naar Zarlino's ontwerp bouwde

Het 19-toonsklavier dat Domenico Pesarese in 1548 naar Zarlino's ontwerp bouwde, voor een middentoonstemming. De witte chromatische toetsen zijn in werkelijkheid rood. (Volgens de bron van dit plaatje zouden het de zwarte toetsen zijn die rood waren, maar dit is erg onwaarschijnlijk omdat er meer klavieren waren met zwarte en rode chromatische toetsen, bijvoorbeeld die van Joan Albert Ban.