|
On chord progressions
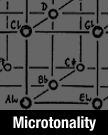
The author examines a variety of chord progressions within tonal harmony. In order to better understand the syntax or `flow' he defends a morphological tool called the Reciprocity Model of chord progression. With this aid he looks at some interesting features mainly oriented around the extended meantone fabric of harmony. I've been a fan of Gesualdo's music since at least the seventies, but only during the eighties did I take the time to examine his harmony in detail. During this same period I also immersed myself in extended meantone (31-et) investigations. Over time I realized that his outrageous chromaticisms make more sense within meantone harmony than they do in the modem system (12-et). He uses mostly simple major and minor chords with relatively few seventh chords, suspensions and linear complexities. Of course, these structures can also be found, but always within a framework of simple chords. Commentators often compare Gesualdo to Wagner in chromatic intensity, but their musical styles prove worlds apart. On the one hand Wagner uses relatively many seventh chords, tritone-removed relations and other features perhaps more at home in 12-et or some shallow (Victorian) well-temperament. He also likes to shift keys rapidly using diminished-related harmonies. On the other hand, Gesualdo practically always stays in the key of G, but roams about wildly to distant functions. Sometimes he creates the illusion that he has modulated, but then he always comes back to the central zone in the end. His notion of functional harmony is quite at variance to that of Wagner. This paper is not about Gesualdo's music in particular, or any other single composer. Rather, it faces this issue: Why do some chord progressions `work,' while others lack direction? In order to find an answer to this question, we need a model that will cover Gesualdo, Wagner, and what lies between. We need a model that makes the `flow' of chord progressions transparent. Of course, voice leading also plays a major role in the estimation and workability of function, but I wish to set this topic aside for now. We need a model with a bit more abstraction that allows a wider perspective. Enter the Reciprocity Model. The name comes from the reciprocal relation (in respect to source) of the Harmonic Series and the Sub-harmonic Series. Being asymmetrical harmonies, the major and minor chord nevertheless has a common parent and a clear functional expression: I and IVm. This special relation forms the 'cross-over' between the realm of major triads and the realm of minor triads. I model these two realms as concentric circles based on the circle of fifths for 31-et. (See the photo-diagram). The two circles are skewed in order to highlight directionality. For example, V resolves to either I or Im. Either way we see a counter-clockwise direction of motion that is characteristic of major mode tonality. In the minor mode tonality IVm resolves to either Im or I, exhibiting a clockwise motion. Directionality colors the mode. Because I and IVm make a reciprocal relation in respect to the source pitch, I and Im form a reciprocal relation in respect to the Harmonic Axis (1 5). These two functions constitute the highest ranking in a hierarchy of relations. In the exemplar of the photo (that I made many years ago) I used the symbol ‘-’ but for this paper I will give it the number ‘0’. Every other function has some number above it that defines its rank (R) in the network of triad chords. Rank 1 consists of V and IVm, chords that form a reciprocal relation along the Harmonic Axis. Apart they prove asymmetrical, but combined they make a symmetrical harmony. So it also is for any equally ranked pair, such as R2 (IV and Vm), R3 (II and bVIIm) and so on. These R numbers make a convenient shorthand in the notation of chord progressions. The R numbers prove fundamental in the model. Looking at the outer circle of major triads, odd numbers (on the dominant side) indicate momentum or centripetal motion towards the tonic. The even numbers (on the sub-dominant side) show centrifugal motion away from the tonic. In an analogous manner for the minor chord circle, odd numbers (sub-dominant side) show centripetal momentum towards the minor tonic, even numbers centrifugal motion away. Because the system has axis orientation, we can use the same numbers to find the analogous progression in the other mode. Here is another reason for the name ‘Reciprocity Model’. For example, take the major mode progression: I VIm IIm II7 V7, in rank numbers 0 6 4 3 1. Note that I have underlined the R numbers of the minor chords for this paper, something that I did not do on the old exemplar. The analogous progression in the minor mode is 0 6 4 3 1, that is Im bIII bVII bVIIm6 IVm6. Thus the Reciprocity Model proves very convenient for comparing and mixing progressions between the two modes of tonality. It shows the way that triad chords (and their seventh chord derivatives) tend to move. The Recipocity Model is not the only device that I have employed for the handling of the two circles. An alternative (that I used for years) I will call the Regional Model. Here I place the VIm directly under the I, lining up the various regions of 31-et. The advantage of this approach centers on the Expansion Index of the circle of fifths. Since I and VIm share the E5 expansion, it becomes very easy to find the E number for any function or relation. This framework goes along with a long-term use of the circle of fifths as a pattern referent. Such information is not so transparent in the Reciprocity Model, where I must calculate each instance individually. Of course, this is not so difficult. Even though the Regional Model is undoubtedly useful, I find the Reciprocity Model far more ergonomic regarding how chords actually behave. Since the eighties I have used yet another model that seems highly promising. I map the patterns on the tri-axial matrix (the Matrix Model), Although it plays no active part in this paper, certain concepts here derive from that approach. Notably, from the matrix for 31-et I have acquired the boundaries for the regions: major, minor, supramajor, flat-minor, sharp-major, semi-major, semi-minor and enharmonic (or antipodal). These names come from the orientation of the tuning system along the major third axis of just tuning, with its attendant ‘meantone corridor’. In the exemplar I have highlighted the boundary functionsthat connect two regions. For example, bVII sits both in the major region and in the minor region. Again, II forms a boundary between the major region and the supra-major (or extended dominant) region. Such highlights help in orientation, but the functions are not intended to have a higher status than surrounding functions. The Matrix Model is specific to each system (here 31-et) but I want the device to be applicable to 19-et and 12-et as well. The Reciprocity Model does quite well in this regard. When working in 12-et, just restrict the functions to rank 12, in 19-et restrict it to 19. Only a minimal change of notation is necessary. In other words, I can use this same device between systems. In the end I refer everything to the 31-et circle of fifths where the elements of the scale (and their derivative pitch names) are highlighted. After all, the function II7 means little unless one knows that it defines the scalar elements 2 #4 6 1 within the key of (say) G, that is the pitches A C# E G. The wheel of fifths where element and pitch can be independently calibrated remains the central tool where everything comes together. But this device itself is not the topic of the paper and I won't dwell upon it here. Focus upon the Reciprocity Model. What can it teach us about tonal chord progression? Firstly it teaches us the inevitability of the shuffle between modes. Many chord progressions begin the minor mode but end in the major (or vice versa). This back and forth alteration occurs very often, especially in renaissance music. Most composers mix functions from the minor mode into the major. Sometimes this mixture of modes becomes so dense that it proves hard to say which mode predominates. Thus I and Im (rank 0, 0) form a collective identity that jointly serves as the point of departure and ultimate goal of tonal progressions. Their close relation is highlighted by their proximity on the wheel. The first true chord progression implicates rank 1 chords: in the major mode we see I IVm V I, in the minor Im V IVm Im. Same chords, only the direction changes. Someone (I forget who) once said that the art of making a good progression consists of finding an interesting way to get from the sub-dominant to the dominant. But don't we go the other way in the minor mode? We can also look at these two progressions in another manner. Both of them form abbreviations of a ‘loop tour’ around the center: in the major I IVm Im V I, in the minor Im V I IVm Im. Such a tour involves both clockwise and anti-clockwise motion. We will see later that many (especially mixed) progressions favor this motion back and forth between the dominant and sub-dominant realms. At least we alternate the two directions of motion. Nevertheless, in the major mode the anti-clockwise motion generally predominates. In the minor mode I would like to say that clockwise motion predominates, but here controversy ensues. Since the minor mode proves less stable, theorists have differing ideas on the normative motion. Indeed, the minor triad and scale has always been the magnet for disagreements, at least from renaissance times. This model favors an equal status between V7 and lVm6, meaning that they serve the same function within the two modes. IVm6 naturally resolves to Im just as V7 resolves to I. They also exchange places with regard to the mode, resulting in a very close relation. They should be treated as equals between the modes. Now this approach is far from universally accepted. Many theorists insist that IVm6 just doesn't have the status or stability of V7 at all. In fact it functions as nothing but a dominant preparation like IV and IIm. Moreover, the progression is not even diatonic - we must use an accidental. A better candidate for `simplest' progression could be I IV V I. In fact, the function IVm6 is so unstable that we prefer to call it the halfdiminished chord (IIob7), even when the element 4 is in the bass. That way its dominant preparation function is emphasized. The Reciprocity Model is plainly deluded by polarity theory – the very name exudes it! I concede that these arguments have merit, yet I hope to persuade you (through the rest of this short paper) that the Reciprocity Model has a certain elegance and balance worth the investigation. To put it bluntly, it works as a guide to the behavior of chord progressions, both in 12-et and 31-et. V7 and IVm6 not only merit a rank 1, they also belong to a special family of seventh and minor sixth chords that act as dominant substitutes. These eight functions make prominent signposts on the wheel and allow us to go very far afield without losing the gravitational pull of the tonality (at least in 31-et). However, we should postpone this discussion until a basis in diatonic progressions is laid out. From there we will move into the central topic of mixed progression, where the family of dominant substitutes become highly relevant. For now let's define the major mode by the ‘natural’ scale also called the Ionian (scalar elements 1 2 3 4 5 6 7). It generates a small family of chords whose normative behavior can be seen in a simple sequence. Theorists traditionally named it the progression by sequence of ‘bass fifths’. It goes I IV VIIo IIIm VIm JIIm V I, rank 0 2 (10) 8 6 4 1 0. None of this is controversial. The novel feature here is the diminished chord (elements 7 2 4), a chord type not even present in our model at all. Accordingly I have used a bracket around the rank number, indicating that it is not really a minor chord and that its presence is only ‘virtual’. Moreover, I also affirm that the farthest rank number of this segment is 8 and not 10. Diminished chords are easy to handle, since they form the essential subset of V7 and thus act as (non-seventh chord) dominant substitutes. Nevertheless, the VIIo is the weakest link in this chain. It has a much stronger tendency to go I IV VIIo I. Even more often it goes I VIIo I, always acting as a sit-in for V7. In our normative sequence, the move from VIIo to IIIm is somewhat more tentative or artificial. Moreover, it sits in the place where a reversal of the normative direction of motion happens (from IV to IIIm). In spite of this weak spot the rest of the progression is robust. We can be forgiven for starting the sequence with IIIm, the farthest rank. Yet the progression I IV also has normative motion, the IV I progression (plagal cadence) requires some effort. The functions IV, IIIm, VIm, and IIm are generally named dominant preparations. Most theorists judge IIm V I (R 4 1 0) to be perhaps the simplest or the archetypal progression. However, this E7 expansion also has a close rival in the E6 pattern VIm V I (R 6 1 0) and its E6 elaboration IIIm VIm V I (R 8 6 1 0). Of course, another contender is VIm IIm V I (R 6 4 1 0). Yet another is IIIm IIm V I (R 8 4 1 0). This group forms the subsets of IIIm VIm IIm V I (R 8 6 4 1 0). What they have in common is a consistent major mode directionality in the anti-clockwise direction, and a movement from larger rank numbers to smaller rank numbers. However, norms are not rigid rules. Progressions also work when they employ a shift of direction. The ‘anti-normative’ motion feels like swimming upstream instead of going with the current. I call it ‘handing’ instead of ‘resolving’. The simplest example can be found in I IV V I (R 0 2 1 0. We feel it in developments such as VIm IV V I (R 6 2 1 0) and in IIIm IV V I (R 8 2 10). In these progressions rank numbers still decrease, a normative feature. Finally, in richer and more complex progressions rank numbers can also occasionally vacillate. We see it in IV IIm V I (R 2 4 1 0), in VIm IV IIm V I (R 6 2 4 1 0), and in IIIm VIm IV IIm V I (R 8 6 2 4 1 0). In spite of the reversals, the general trend is toward a decrease in rank numbers. A persistence in going upstream stores a load of potential energy that wants release. Play I V IIm IIIm (R 0 1 4 8) and feel the urge to resolve to VIm or to IV. As another more complex example of mostly building, try the scalar-order progression I IIm IIIm IV V VIm VIIo 1 (R 0 4 8 2 1 6 (10) 0). It expresses a certain tension that wants resolution. As far as I have seen, theorists agree on all of this. Everyone also agrees on the character of the actors. VIm is a sort-of ‘tonic substitute’, such a close relation to I that we call it the relative minor, It synchronizes the major and minor regions. The union of I and VIm makes a major sixth chord IM6 (elements 1 3 5 6), a strong harmony that is like combining two positions on the wheel. However, VIm is not the only tonic substitute. IIIm also has this ‘stand-in’ character, since it makes the first minor triad to appear on the harmonic series. This feature explains why the move from IIIm to IV is normative. The union of I and IIIm also forms an important harmony, the major seventh chord IM7 (elements 1 3 5 7). Some theorists argue that IIIm is not a direct dominant preparation because it is the relative minor of V. Consequently it must work through an intermediary like VIm or IIm. The IIIm function is indeed special because it has the farthest position in the sequence. The function IIm is also special but for different reasons. Definitely not a tonic substitute, it embodies the character of a dominant preparation to a peculiar intensity. Moreover, it sits in the ‘middle ground’ of the movement (rank 4 is halfway to 8). It tends to form an intermediate goal on the way to V or to I. In addition, its seventh-chord elaboration IIm6 (elements 2 4 6 7) belongs to that special family of dominant substitutes whose partner is V7 (5 7 2 4), Here it forms a recessive version of the dominant. Both contain the subset diminished triad (7 2 4). This explains why the progression 11m7 11m6 I works. It has this special ability while still maintaining its preparation status, for example in Vim IIm6 V7 I. Lastly, it forms the relative minor of IV, itself a dominant preparation. Later we must say still more over IIm. I have looked at the Ionian scale in some detail in order to demonstrate the considerations involved in constructing tonal progressions. But the Ionian is not the only major mode. Consider the Lydian (elements 1 2 3 #4 5 6 7). It has its own natural sequence: I# IVo VIIm IIIm VIm II V I (R 0 (12) 10 8 6 3 1 0), I will not bother to write out every progression permutation, it's easy enough to work out. Like in the Ionian version, the diminished triad is the weak link, a chord that points to V rather than to I. Indeed, it is a substitute for II7 rather than V7. The chord sits within the ‘big jump’ from I to VIIm. In spite of the differences, the set behaves just like the Ionian set -same directionality and tendencies. As an example progression, try I #lVo I VIm II7 V I (R 0 (12) 0 6 3 1 0). Note that the scale has no V7, only V. During the 15th century when the Lydian mode came into popular use, Dufay often used the unusual cadence formula VIIm I. The function VIIm is another actor that will provoke more discussion, but it is enough to mention here that it makes the farthest ranking (10) within the much-used diatonic modes. The Mixolydian forms another type of major mode, but I will consider it later with the Dorian minor. First let's tackle the thorny issue of the ‘natural’ minor mode. The cosy consensus seen above breaks down when one ponders the ‘natural’ or Aeolian minor scale (elements 1 2 b3 4 5 b6 b7). What is the normative sequence? According to the Reciprocity Model the answer is simple enough: Im Vm IIo bVI bIII bVII IVm Im (R 0 2 (4) 8 6 4 1 0 ). Note how the rank numbers reproduce the same sequence found in the Ionian major scale, except for that `virtual' factor - the diminished triad. Rank 10 is exchanged for 4 (both of them prominent positions). The IIo chord (elements 2 4 b6) forms the essential subset of IVm6 and acts as a (non seventh chord) sub-dominant substitute. As usual, it makes the weak link in the sequence, separating the `jump spot' between Vm and bVI. It has a strong tendency to prefer Im Vm IIo Im. All of the other structural features also mirror the major mode. For example, rank 4 also acts as a sub-dominant preparation as well as a recessive alternative to IVm6. Rank 6 is also a tonic substitute, called the relative major. Im and bIII unite to form the strong harmony Im7 (elements I b3 5 b7). Rank 8 also makes a tonic substitute, derived from its place in the Sub-harmonic series. Im and bVI unite to make Imb6 (elements 1 b3 5 b6). The parallel is complete. Only the directionality has reversed - the norm for resolution is now clockwise motion. The elegance of this logic is quite compelling. However, most of the theoretical texts that I have consulted over the years give a different sequence of bass fifths: Im IVm bVII bIII bVI IIo V Im (R 0 1 4 6 8 ( 4 ) 1 0 ). It leaves me dissatisfied for several reasons. First of all, it is not even diatonic but rather a mixed progression, because of the inclusion of V from the major mode. Of course it's common to bring V, IV and VIIo into the minor mode, but that is beside the point here. We want a sequence for the diatonic minor mode, not a mixed progression. My second complaint is related to the first: the Vm of the minor scale has been entirely neglected. Thirdly, it feels to me like a ‘building’ sequence rather than a ‘resolving’ one, being strong in the anti-clockwise direction. Fourthly, consider its complexity in comparison with the Reciprocity sequence. It appears to be designed mainly to show off the usefulness of IIo as a dominant preparation - remember that IIo can easily become IIob7, the alter-ego of IVm6. For all of these reasons the Reciprocity Model appears clearer and more consistent to my judgement. The problem arises from the taboo (I cannot find a better word) against the use of the function IVm6. Function is certainly influenced by the voicing of a chord. Thus when the element 2 sits in the bass it becomes feasible to call it IIob7 (elements 2 4 b6 1). However, even when the 4 sits in the bass most theorists call it a ‘first inversion’ half-diminished chord, rather than IVm6 (elements 4 b6 1 2). To be sure, IIob7 acts naturally as a dominant preparation, since the progression is equivalent to the rank 1 progression IVm6 V7. But it can just as naturally resolve to Im (or to I). Concerning the taboo, consider this perfectly analogous situation. Say that the V7 function (elements 5 7 2 4) must be renamed VIIob6 (elements 7 2 4 5). Then when 5 sits in the bass we must call it a ‘fourth inversion’ VIIob6. The reader will surely find this example absurd, but the case of 11ob7 and IVm6 is just as absurd. The parallelism between the ‘natural’ major and ‘natural’ minor modes is total. Every progression that I have presented in the Ionian mode finds a corresponding progression in the Aeolian mode that uses the same rank numbers and that matches it in structural characteristics and tendencies. Only the directionality is reversed. I will not repeat the many sample progressions already given - only one, the complex scalar-order progression. It serves as an example of the isomorphism in the rank numbers. The progression goes: Im bVII bVI Vm IVm bIII IIo Im (R 0 4 8 2 1 6 (4) 0). Only the ‘virtual’ factor is altered. The strength of the Reciprocity Model lies in the ease of finding such parallel structures between modes. The Aeolian mode is not the only minor mode. In the Phrygian minor (elements 1 b2 b3 4 5 b6 b7) we can recognize the ‘mirror’ of the Lydian major. Its sequence by bass fifths goes: Im Vo bII bVI bIll bVIIm IVm Im (2) 10 8 6 3 1 0). Here the Vo (elements 5 b7 b2) forms the essential subset of bVIIm6 (elements b7 b2 4 5). Just as the Lydian mode is the ‘most major’ with the farthest ranking of 10, so here the Phrygian is the most minor with farthest ranking 10. The sample progression that I gave in the Lydian mode finds its parallel here as: Im Vo Im bIII bVIIm6 IVm Im (R 0 (2) 0 6 3 1 0). The Locrian minor mode (elements I b2 b3 4 b5 b6 b7) forms a special case in which there is no harmonic axis (1 5). Instead it uses 1 b5. Consequently it becomes unstable and is little used in this position. We can see the problem by examining its sequence: Io bV bII bVI bIIIm bVIIm IVm Io (R (0) 12 10 8 5 3 1(0)). The diminished triad falls on the tonic position where it forms the essential subset of bIIlm6. Thus it has no diatonic resolution. It also sits on the edge of what is possible in 12-et with its rank 12. Finally, it has no mirror in the major mode without destroying the tonic function. However, it can still be integrated into mixed progressions with ease. Given the mirror-like structural relationship between the Ionian and Aeolian modes, and again between the Lydian and Phrygian, we would expect a similar relationship between the Mixolydian major and Dorian minor. We are not disappointed. The sequence for the Mixolydian major mode (elements 1 2 3 4 5 6 b7) goes like this: I IV bVII IIIo VIm IIm Vm I (R 0 2 4 (8) 6 4 2 0). The IIIo (elements 3 5 b7) acts as the essential subset of I7 (elements 1 3 5 b7). The sequence for the Dorian minor (elements 1 2 b3 4 5 6 b7) goes: Im Vm IIm VIo bIII bVII IV Im (R 0 2 4 (6) 6 4 2 0 ). The VIo (elements 6 1 b3) acts as the essential subset of Im6 (elements 1 b3 . These two modes have peculiar properties. Notice that the one is almost the reversal of the other. The numbers form almost a palindrome. The sense of normative direction is still there but weakened somewhat, since the balance between the dominant and sub-dominant realms is so evenly matched. In these two modes the rank 2 chords become very prominent, for example in the Dorian Im Vm IV Im (R 0 2 2 0) and the Mixolydian I IV Vm I (R 0 2 2 0). Here the wobble between the major and minor modes is particularly acute - they come so close to each other. Even more significantly, these modes pool the rank 4 chords as in the Mixolydian I bVII IIm I (R 0 4 4 0) and the Dorian Im IIm bVII Im (R 0 4 4 0). Sitting in the recessive dominant power position, these progressions naturally become bVII IIm6 I and IIm bVII7 Im. The pair of harmonies has yet another unique feature: rank 6 as the furthest mark. They enclose a region bounded by the relative minor relation. To summarize: the three pairs of diatonic modes express a rank 6, 8, and 10. Such numbers are obviously part of a bigger picture whose theoretical underpinnings I must yet elucidate. All in good time. First we ease our way into mixed progressions by following the old road of extended dominants. Extended dominants act as chromatic extensions of the diatonic norms so that the supra-major region is brought into the major region - all within the major mode, of course. It makes use of the tendency for V7 to resolve either to I or Im. The supra-major or extended dominant region sits between ranks 3 and 11. In the middle of the region resides rank 7, the III7 that goes to VIm (R 7 6). At the inner boundary sits II7 so that 4 1 0 becomes 3 1 0. The approach is versatile because both resolutions work. For example, VI7 can become IIm (R 5 4) or II (R 5 3). The numbers mutate beautifully. The whole network is also prone to extended sequences like R 7 6 5 4. The outer end of the region in ranks 9 and 11 are closely tied to the key position, rank 10. A push beyond these borders into the sharp-major region yields largely unexplored territory where the extended dominants relate more closely to the power position 16. We will go there later, but first we must ponder the extended subdominants. The flat-minor region (or region of extended sub-dominants) is integrated into the minor region through chromatic extensions of the diatonic norms. Since IVm6 resolves either to Im or to I, the same sort of sequences as those shown above make good progressions. In the middle of the region (which runs from R 5 to 13) sits rank 9, the bIIm6 that seeks bVI (R 9 8) or possibly bVIm (R 9 7). At the outer boundary terra incognito looms as far as traditional music theory is concerned. The concept of a region of extended sub-dominants has never taken a firm hold on traditional tonal theory. Evidently this is because, in 12-et, all that one really needs are three regions: minor, major, and supra-major. Of course, we could also choose major, minor, and flat-minor and it would work just as well. The 12-et system is bound by rank 12-tritone relations. It is a zone of boundaries where enharmonic differences are erased. 31-et tells a more subtle story. The approach of extended dominants has its charms, but the traditional view of mixed progressions involves a mixing of the local major and minor regions - not some far away outer region. Now we have the renaissance approach. Of course, for the style that Gesualdo pursued, he used a wider field than that. In order to feel comfortable in this world we need an overview of the wider possibilities. It's time to get theoretical! After many years of deliberation, I see it like this: eight ‘power spots’ or special positions control the way that progressions develop. These cardinal points arise out of the alternative harmonization of the two normative tritones (functional elements 7 4 and 2 b6). The basis lies in the tritone because here we find the source of that stress or drive to resolution that one sees in V7. But that same stress can also be found in three more places that hold the (7 4), four that hold the (2 b6). The hot-spots are 1, 1, 4, 4, 10, 10, 16 and 16. This information, including the all-important functional elements of the scale, is best laid out in a table - the complete list of the normative dominant and sub-dominant substitutions. 16 bIV-7 (b4 b6 b1 2) bIV-7#4 (b4 b6 b7 2) bIV-7#5 (b4 b6 1 2) 10 bII-7 (b2 4 b6 7) bII-7#4 (b2 4 5 7) bII-7#5 (b4 b6 1 2) 4 bVII7 (b7 2 4 b6) bVII7b5 (b7 2 b4 b6) bVII7#5 (b7 2 #4 b6) 1 V7 (5 7 2 4) V7b5 (5 7 b2 4) V7#5 (5 7 #2 4) 1 IVm6 (4 b6 1 2) 2 IV-7#4 (4 6 7 #2) 4 IIm6 (2 4 6 7) 3 II7b5 (2 #4 b6 1) 10 VIIm+6 (7 2 #4 b6) 9 VII7b5 (7 #2 4 6) 16 #Vm+6 (#5 7 #2 4) 8 bVI-7#4 (b6 1 2 #4) The order of the table follows the sweep from left to right - first the major chord circle, then the minor chord circle. This order results in more flats at the top, more sharps at the bottom. The table has three columns in order to also accommodate the altered dominants (7b5 and 7#5) whose structure is intimately bound up with the seventh chord norms. Thus the altered dominants also form an integral part of the family. In the order of the table, the minor (2 b6) and major (7 4) subsets alternate: the (7 4) is found in 10, 1, 4, and 16; while the (2 b6) resides in 16, 4, 1 and 10. Sorry, but at this point we must leave 12-et behind. It just cannot make rank 16 at all. It attempts to simulate it with rank 7, but III7 has much different directional tendencies than bIV-7. For 12-et rank 10 is furthest ‘out’. On the other hand, 19-et can well accommodate the whole family. However, ranks 10 and 16 both prove to be entirely antipodal, the most advanced harmony of the system. In 31-et the family covers about half of the circle - 16 and 16 are antipodal to each other. Why not go further? The most advanced harmony of 31-et lies beyond this border. The antipodal zone kicks in around ranks 23 and 24, with its center in rank 30. The antipodal zone is surrounded by a septimal zone centered in ranks 19 and 20. But this sort of harmony is too complex an issue to consider in this short paper. My interest here lies in traditional tonal harmony oriented around the major and minor modes. Consider first the (7 4) relation. It has a bias for the major resolution, but accommodates the minor quite well. Four functions contain it: V7, IIm6, bII-7 and #Vm+6. The first two form the diatonic pair, the second two the septimal pair. V7 makes the assertive diatonic dominant, while 11m6 forms the recessive diatonic dominant substitute. Similarly, the septimal pair also makes assertive and recessive forms. These four functions are easily transformed into each other because they all have two elements in common (7 4). Even more importantly, they tend to take over each other's roles, making ‘short cuts’ or end-runs to the tonic resolution. Thus IIm6 acts as a dominant substitute in the progression IIm6 I, while it also acts as a dominant preparation in IIm6 V. Similarly, bII-7 acts as a dominant substitute in bII-7, (usually called the tritone-removed resolution), but it also acts as a dominant preparation in bII-7 V. Lastly, #Vm+6 acts as a dominant substitute in #Vm+6 I and also as a dominant preparation in #Vm+6 V. Moreover, the close structural relations between these harmonies also make sequences possible: for example, the progression IIm6 bII-7 I or the progression #Vm+6 IIm6 V. Now consider the (2 b6) relation. It has a bias for the minor resolution, but stays happy with the major as well. Four functions contain it: IVm6 (assertive diatonic), bVII7 (recessive diatonic), VIIm+6 (assertive septimal) and bIV-7 (recessive septimal). In parallel to what we see above, bVII7 acts both as a sub-dominant substitute (bVII7 Im) and a sub-dominant preparation (bVII7 IVm). The VIIm+6 also acts as a triton-removed substitute (VIIm+6 Im) and a preparation (VIIm+6 IVm). Finally, bIV-7 acts as a substitution (bIV-7 Im) and a preparation (bIV-7 IVm). Again, these four functions can easily be transformed into each other due to the common (2 b6). They also make sequences, such as bVII7 VIIm+6 Im and bIV-7 bVII7 IVm. Because these two groups of functions are ‘tolerant’ of each other, they also work together between the groups. For example, we see it in VIIm+6 V7 I or in bII-7 IVm6 Im. Thus they form an integrated family of eight possibilities that can interact in different ways. Of course, these seventh chords are not the only structures to contain (7 4) and (2 b6). However, I have chosen (in the interest of brevity) to ignore complex linear chords, suspensions, etc. They can best be approached as modifications of the eight norms. In the following section where I will examine some historical progressions, I have occasionally simplified them somewhat in order to ignore such linear complexities. However, I do need to mention a few additional structures that surface in the examples and, indeed, have special associate status. The first two are the diminished triads VIIo and IIo, who share the same resolution bias and also sit ‘virtually’ on the magic spots 10 and 4. They belong to the group as close friends. Another pair that belongs here is the symmetrical V7,2 (elements 5 6 7 2 4) and IVm6,4 (elements 4 b6 b7 1 2). They form the aggregate union of 1 and 4 in the V7,2 and the merging of 1 and 4 in IVm6,4. The last pair that has associate status forms an aggregate union of rank 1, 1 and the diminished tetrad (10). In V7,b2 (elements 5 b6 7 2 4) the 1 and (10) unite; while in the IVm6,#4 (elements 4 b6 7 1 2) the 1 and (10) unite. These examples illustrate that supersets of the diminished tetrad in combination with one of the norms results in more complex but related structures. The diminished tetrad VIIo7 (elements 7 2 4 b6) is an extra-ordinary harmony that deserves special status. It sits ‘virtually’ on rank 10. It combines the VIIo and the IIo to form a structure that has absolutely no bias. Thus it is fundamentally different from all the other harmonies mentioned so far, who all exhibit a resolution bias. Yet an examination of the table reveals that all of them consist of some (often only minimal) modification of the diminished tetrad. Note that the set of harmonies on the major circle (1, 4, 10, 16) even forms a diminished tetrad relation with each other - the same for the minor circle (1, 4, 10, 16). In short, the diminished tetrad VIIo7 is the sovereign of this set and the table is its kingdom of subjects. I need to say a little about the altered dominants, in order to justify their inclusion in the family. The 7b5 group of four functions form a special symmetrical structure that (like the diminished tetrad) has two tritones and (uniquely) two functional names. For example, V7b5 (elements 5 7 b2 4) shares the same information as bII-7#4 (elements b2 4 5 7). In fact the harmony combines parts of both, not in an aggregate union (like V7,2) but a selective union. The result is a harmony with aspects of both V7 and bII-7, a working together of the assertive team of diatonic and septimal harmonies. Similarly, in bVII7b5 and bIV-7#4 the recessive team works together. In a more complex modification (evident through the rank numbers), the assertive team IV-7#4 and VII7b5 work together, as do the II7b5 and bVI-7#4. These functions exhaust the possibilities for the placement of the normative tritones in the 7b5/-7#4 group. Of course, the altered dominants behave according to the rank numbers of their unaltered norms. Thus II7b5/bVI-7#4 normatively goes to V (or Vm) while, oddly enough, VII7b5/IV-7#4 tends to III (or IIIm). Such functional complexity results from the double tritone. The asymmetrical 7#5 group does not have double names, but it does display the same ‘cooperation’ seen in the 7b5 group. For example, V7#5 mediates between V7 and #Vm+6, a mediation between an assertive diatonic and a recessive septimal. bIV-7#5 mediates between IVm6 and bIV-7, also an assertive diatonic and a recessive septimal. Again, bII-7#5 mediates between IIm6 and bII-7, a recessive diatonic and an assertive septimal. Finally, bVII7#5 mediates between bVII7 and VIIm+6, also a recessive diatonic and an assertive septimal. Thus, like the 7b5 group, the 7#5 group brings together disparate power positions and forms an integral part of the substitution family. In the last section we saw how the type 1 relation could be transposed to various positions as extended dominants, in order to direct the progression toward some goal. Well, the same thing can be done with the other relations of the table. This is the central thesis of my paper. With these powerful tools we can explain much of what goes on in wide ranging progressions. For now I will give just a couple of historical examples. In the so-called German augmented sixth chord resolution bVI-7 V we see the same relation as bII-7 I, the tritone-removed substitution. In the same way we could make bV-7 IV. By the way, the bVI-7 (elements b6 1 b3 #4) was sometimes used without the fifth (to avoid parallel fifths), yielding (b6 1 #4). In this case it was renamed the Italian sixth chord. We should note here that the harmonies of the table can also be culled in a similar manner. The second example is the so-called deceptive cadence V7 VIm. Usually it is explained as the substitution of the relative minor in place of the normative I. But it can also be explained as an example of the bVII7 Im type resolution. Type 4 relations can be strung together in sequences, for example in this progression with a somewhat Dorian-Mixolydian character: Im Im6 bVII IV7 Vm IIm6 I (R 0 0 4 2 2 4 0). Many further examples could be given where the tendency of the progression is governed by one of our dominant substitution relations. The table offers valuable information on how to handle distant functions. Take for example the #Im (elements #1 3 #5), rank 14. It has always posed problems for theorists because it seems to be distant from both the major and the minor sphere of influence. What can be done with it? Well, one can invoke #Im6 (elements #1 3 #5 #6) and resolve it to #Vm+6 and hence within contact of the tonic. Alternatively one can use #Im6 and (by a type 4 resolution resolve it to VII7 that then moves to IIIm. Another more direct alternative is #Im+6 17 IVm. Here the septimal version #1m+6 (elements #1 3 #5 b7) poses a different tendency than #1m6. The 31-et distinction between diatonic and septimal seventh chords makes distant functions more easily integrated into the tonal fabric. Returning to the local regions, we are ready to examine the concept of the mixing of modes. Historically, many theorists have proposed that the `foreign' modal substitution should behave in the same way as the original. But this is just not so. The mixture redirects the progression into a new direction. What proves important here is that the relation between the substitute and the original also involves our special family of relations. Let's look at some examples. In the progression I VIIm bVII7 IV IVm V7 (R 0 10 4 2 1 1) the foreign element bVII7 replaces VIIm. For that matter, it could also have replaced VIIo7 or VIIm+6. Either way, the relation between the original and the foreigner sits on our power positions 10 and 4. Alternative substitutions also use a transposition of the same relation. For example, in I IIIm bIII IV V7 (R 0 8 6 2 1) we see it in the relation between IIIm and bIII. Again, in I Vim bVI7 bVIIm I (R 0 6 8 3 0) it sits between VIm and bVI. In I VIm IIm bII-7 IVm6 I (R 0 6 4 10 1 0 ) the relation again sits on the power spots 4 and 10. A final darker example, I Vm bV7 bVIm b1117 IVm Im (R 0 2 12 7 6 1 0). Here the aspects of the minor mode have largely taken over. In these examples we have interpolated foreign elements into the major mode to redirect it, but we get similar results by substituting foreign major elements into the minor mode. The substitutions given above reflect traditional practice, but the movement can be extended in either direction. For example, take Im bI or again IVm bIV that inhabits the power positions. Going in the other direction we have IV #IVm, or again I #Im, and V #Vm on the power spots. Thus the concept of the mixing of modes uses one distant but special relation that we can define as a type 14 change. This movement always brings us into the adjacent region. The two dominant substitution positons bIV and #Vm form the endpoints of a ‘central zone’ where mixture is most common. Not surprisingly, this zone is dominated by a diminished tetrad structure. Follow the sequence 16 1, then 10 4, then 4 10, then 1 16. Of course, the relations directly governed by dominant substitutions don't explain every type of normative movement. Progressions that avoid tritone-bearing chords have somewhat more leeway in direction, less fixation on a particular outcome. In this environment the importance of the power positions are still evident but different rank positions also gain in prominence. A systematic theoretical structure should lay out the characteristics of every rank position. Unfortunately, such a project is beyond the scope of this essay - we will stick to the smaller numbers. Every movement from one chord to another involves some type of change that can be conveniently defined by the rank number. For example, the changes I IIm and V VIm both express a type 4 movement from the major to the minor chord. As we saw above, the relation we associate with the mixing of modes as exemplified by VIIm bVII expresses a type 14 movement. Generalizing this procedure we can map out the relations between the entire set of major and minor chords. One useful way of grouping these various ranks involves their Expansion Index on the circle of fifths. Take the relative minor progression from I to VIm (R 0 6) and its complimentary direction, the relative major progression VIm I (R 6 0). Together, both harmonies share an E5 expansion. Rank 6 and 6 are unique in their E5 expansion. When we allow an E6 expansion four ranks fit within this compass. This information is best laid out in a small table. The left-hand column shows movement from the major chord, the right from the minor chord.
I have not extended the table very far (E 11), just far enough to illustrate a general principle: ranks with lower E numbers would tend to get more usage (statistically) in traditional harmony than ranks with extremely wide expansions. Such distant movements prove more exotic or unusual. We can best illustrate these principles by examining some historical examples. What follows is some brief commentary on a small sample of historical progressions that have caught my attention. They are either unusual, ingenious, or illustrate some structural interest. I present them in no rigid historical order, Moreover, I do not claim comprehensibility in such a small sample. Although little more than a glimpse, we still see the continued usefulness of the Reciprocity Model. Around the very dawn of the 16th century Josquin Despres composed this mixed progression which was (for his time) quite progressive. It occurs in the ending segment of Absolon fili mi. In the key of G, starting in the major mode he makes a sequence of 6 and 8 movements. By this ‘back and forth’ motion he travels far into the minor region, then resolves it into the ‘empty’ tonic (the harmonic axis 1 5). The progression takes this route: I VIm IV IIm bVII Vm bIll bVI IV Im6 Im7 V I(m). In rank numbers it comes to 0 6 2 4 4 2 6 8 1 0 1 0. The function bVI forms his furthest point of travel. The ambivalent ending is typical of renaissance music. The composition as a whole favors the minor mode but often sits in the major. The sequence of the types of changes can be defined as 6 8 6 8 6 8 2 6 2 1 2. In the last change I have used V I which is a type 2, while the alternative V Im is a type 1. The replacement of the major or minor chord by the naked harmonic axis is quite prevalent in the 15th and 16th centuries. The sequence of 6 and 8 movements is wonderfully interlocking, a characteristic most graphically seen on the tri-axial matrix. Note that all of the types of changes used in this progression use only E5 or E6 expansions (ignoring the solitary seventh chord IVm6 that will inject an E7 factor). From my anecdotal experience, a big fraction of 16th century music sits in the key of G but uses a key signature of one flat-making the dorian mode its ‘home’ scale. Perhaps this practice is a conservative carry over from medieval theory, where the dorian scale is the ‘first’ mode. This orientation also reflects and supports the traditional meantone setting of a line of fifths from Eb to G#. The progression above fits like a glove into this keyboard orientation. Desire to expand the line of fifths into wider territory led to ‘split’ keyboards, culminating in Vicentino's instrument with Luzzaschi as its virtuoso performer. Moving to the 19th century, Brahms (in his Requiem) composed a truly brilliant progression. Using the same sequence that we have seen above and adding only one additional ‘trick’ he manages to swing all the way around the 12-et circle of fifths. The sequence goes Im7 bVI IVm bII #IVm II VIIm V IIIm I. In rank numbers it goes: 0 8 1 10 12 3 10 1 8 0. He has employed 12, the maximally distant function for 12et. The main interest here lies in the move from bII to #IVm. For, having reached bII far in the minor region, he simply redefines it as #I (R 13) so that it naturally moves to #IVm. The 12-et tuning system makes such operations easy. This progression is often touted by theorists as proof of a passage that can only be played in 12-et; it just can't be done in meantone. However, this statement just isn't true. One can well move from bII to #IVm in meantone, but we must be willing to take a big jump. In fact, it is an E13 movement involving an enharmonic shift. This can be seen from the elements of bII (b2 4 b6) and #IVm (#4 6 #1). The other tones move by a chromatic semitone, which is fluid enough. The presence of an enharmonic shift is enough to make most theorists reject the sequence, but when one thinks about it the efficacy of the move comes down to an attitude. During the late 16th century such progressive composers as Vicentino and Gesualdo sought out such exotica intentionally for their effect. If we were to play Brahms' progression in 31-et the move from bII to #IVm expresses a type 22 rank in E 13 - definitely an unusual move just beyond the limit of my little table above. The rest of the progression is strictly in sequence. It goes 8 6 8 22 8 6 8 6 8. Thus he has expanded on Josquin's sequence by using a special connector. Elsewhere in the same composition Brahms provides another more elided version of his trip around the circle. It goes Im bVI7 bII VIIm V7 Im (R 0 8 10 10 1 0). Again he redefines bII as #I, but this time the jump sits between the two power spots 10 and 10. Now we have a distance of type 20 which has E 12. In his manuscript not only did he spell bII as #I, he also renamed bVI7 as #V7. Such sleight-of-hand is convenient in 12-et but it is nevertheless illusory. Coming from the minor mode the chords clearly function as bII and bV17. The sequence of changes in 31-et would be 8 2 20 8 1. Relating to 31-et performance, the bVI7 is perhaps better as bVI-7 in anticipation of the jump, but then it could also be defined as bVI7 acting as extended dominant to bII. More effectively in the interest of enhancing functional clarity, the big jump itself can be softened by using bII-7 and VIIm+6 instead of bII and VIIm. The 12 function seen in Brahms was already in use by the middle of the 16th century. For example, it occurs in this passage from the madrigal O morte, eterno fin by Cipriano de Rore. I VI #IVm VIIm V Vm VIm IV VIm II. In rank numbers we have 0 5 12 10 1 2 6 2 6 3. The progression is unusual in its closure at II rather than V or I. A classical composer confronted by VI is likely to treat it as an extended dominant that resolves to IIm, but instead Rore invokes a 6 movement taking it yet further away. Then he fills in the space between using various colorful jumps. The changes can be defined as 5 6 1 8 0 4 8 8 1. Although these particular changes are not very unusual, Rore sometimes employs some quite exotic jumps, for example Im VI, an E11 movement. Such jumps became more common in Gesualdo. Indeed, Rore is an important originator of Gesualdo's wayward style, although Luzzaschi influenced him more directly, In Rore we see for the first time the need to expand the line of fifths beyond twelve in a single composition. Consider this famous passage from Wagner's Parsifal - the harmonization of the main theme. It goes bV IIm bV IIm V7 I bVIm Im (R 12 4 12 4 1 0 7 1). The progression shows how a very ‘distant’ progression can be constructed by using a tritoneremoved substitution. The bV replaces I, transforming a conventional diatonic progression into chromatic complexity. The bVIm function is even more interesting. One is tempted to derive it by tritone-removal from IIm, but the direction is wrong. In that case he should have spelled it #Vm. However, I think that he really meant bVIm, a function that conventionally moves to bIII, but here it goes to its relative minor. This progression shows how important tritone-removed functions are to Wagner's style. Consider this passage from Bach's chorale Herzliester Jesu, was halt du verbrochen. It has a somewhat mixolydian feel due to the importance of Vm and IV. It goes: Im II7 Vm IV7 Vm bVII7 IIIo7 bVIIm I (R 0 3 2 2 2 4 (8) 3 0). The II7 acts as an extended dominant to Vm. The IIIo7 bVIIm progression is quite unusual since the diminished tetrad normally resolves to IV(m). But IIIo7 (elements 3 5 b7 b2) has two scalar elements in common with bVIIm (b7 b2 4). Though unorthodox it still works out. The progression bVIIm I is also a rather uncommon cadence. In spite of the novelty of the 3 and 3 functions the passage still manages to maintain that narrow compass characteristic of mixolydian-dorian progressions. We see a predominantly phrygian mood in this passage that ends Willaert's madrigal Mentre che'I cor. It goes: bVIIm bV IVm bVIIm IVm bVIIm bVI IVm I (R 3 12 1 3 1 3 8 10). The bV represents a diversion into Locrian territory. The progression bV IVm shows a type 10 change that could be further defined by using the septimal bV-7, In spite of the minor mood, the piece ends in the major - a prevalent practice during the 16th century. In this passage from the madrigal Signor le tue man saute by G. Gabrieli we see a characteristic focus on the ‘power spots’. The progression goes: I IVm I IVm Im V Im V Im I IVm bII bVIIm IV (R 0 1 0 1 0 1 0 1 0 1 10 3 2), The progression is directed toward IV but emphasizes the reciprocal relation I IVm. This same relation is repeated between Im V and later between bVIIm IV. These 1 and 1 relations are very much used in renaissance music, more than in classical or romantic period music. Note how well they suit the Reciprocity Model. This excerpt from Wolf's Zur ruh, zur ruh is expanded by various linear complexities, but its skeleton of seventh chords goes IV7 bVII7 I7,b2 Im (R 2 4 0 0). The interest here lies in the I7,b2 that does not resolve conventionally to IV(m). Instead it moves to Im, illustrating that constant use of tritone-bearing chords weakens the functional intent. Consequently the chords get used more for local color than for function. The price one pays is a more ambivalent tonality. Such overloaded harmony led to the subversion of tonality by the end of the 19th century. In Beethoven's Bagatelle op. 126/3 sits this interesting progression. It moves thus: bII bVI7 bII bVI7 V7 Im (R 10 8 10 8 1 0). The first bVI7 acts as a dominant in order to stabilize the neapolitan bII function. In the second instance the bVI7 acts as a ‘German sixth’ chord to V7. If we played this passage in 31-et the functions could be further clarified by using bVI7 in the first instance and bVI-7 in the second. We can approach this progression as a derivation of tritone-removed relation_s, since bII comes from V while bVI7 comes from II7. Much of advanced harmony from the 19th century follows this pattern. The ‘German sixth’ function already appears during the renaissance period. An early example can be found in Gesualdo's madrigal Io fur respiro. In Dm he makes the progression 1Vm bVI-7 Im V, then he repeats it again in Am. Gesualdo has interpolated the Im but his goal is nevertheless V. Thus the bVI-7 still acts as a ‘German sixth’. From his notation (that uses the scalar elements #4 and b6) it is clear that he intended the septimal harmony. Gesualdo uses block progressions that he transposes rapidly to different keys. However, these are not transpositions in the conventional manner using a pivot chord and other connectors. He juxtaposes them for their shock value. This style is already evident in Vicentino. For example, on just one page of his madrigal 0 messaggi del cor he moves from Eb to Gm to Em. Each section has a relatively conventional progression, but the juxtaposition of them in such disparate ‘keys’ requires a keyboard with both flats and sharps. This colorful wide-ranging style also inhabits the work of Cipriano de Rore. In his madrigal De le belle contrade he presents a progression in A, immediately followed (with no pivot or any preparation) by a progression in distant Cm! Such a juxtaposition is quite revolutionary in its harmonic daring and lays the basis for Gesualdo's work. We can further illustrate this colorful style by a passage from Luzzaschi's madrigal Quivi sospiro. It goes bIII bVI I IV bVI I (R 6 8 0 2 8 0). All the chords are major; moveover, all the chords after the initial bIII have the scalar element I as part of the structure. In spite of these restrictions he makes a progression that jumps back and forth between the major and minor regions. Occasionally these jumps become wide enough to span the minor and supra-major regions. This style of big jumps and alternating regions culminates in Gesualdo. A prominent example occurs at the very beginning of the madrigal Morro lasso al mio duolo. In Am it goes III Im II bVII V7 Im (R 7 0 3 4 1 0). The movement from III to Im is unprecedented, an E12 expansion of rank 7. It even incorporates a ‘wolf’ fourth interval between C and E#. He then proceeds to fill in this wide space with intermediate positions. Here he focuses on the two boundary functions II and bVII, where he adds a linear complexity before resolving it to the dominant. The progression as a whole is loaded with mediant relations and regional jumps. Such progressions lose some of their character when played in 12-et rather than 31-et. Elsewhere in the composition he makes some extra-ordinary progressions. For example, these two juxtaposed blocks move in parallel as IVm to V, then as Im to II. The first block goes: IVm bVI bVII7 bVIM7 bII bVI7 bIIM7 V (R 1 8 4 8 10 8 10 1). He keeps coming back to the 8 function, but each time it has a new variant: bVI, then bVIM7 (a union of bVI and Im), then bVI7. The movement from bVII7 to bVIM7 is quite ingenious. By a type 4 dominant substitution resolution it should normatively move to Im. Instead it goes to bVIM7, a chord in which Im hides. Having used the 4 power position he moves on to the 10 power position where the following bVI7 is its dominant seventh preparation. From his notation it is clear that he means bVI7 and not bVI-7 in anticipation of his jump to V. The bVI7 resolves conventionally to bII but Gesualdo thickens it with bIIM7, a function with a hidden IVm. Then he makes that extra-ordinary leap from bIIM7 to V, a rank 11 change in E 11 (the distance between b2 and 7). A more conventional composer would go from bII-7 to I. By using bIIM7 he has combined the two power spots 1 and 10 and yet avoided the characteristic tritone altogether. Instead of the normative I resolution he uses V, expressing the tritoneremoved relation between bII and V. A more conventional composer would also use the bII-7 in tritone-removal from V7. Gesualdo's use of bIIM7 illustrates why theorists describe his style as ‘manneristi’' or downright eccentric. I would describe it as just plain brilliant. The second block presents the same progression in parallel, this time from Im to II. But the parallelism is not quite exact. It goes: Im bIII IVm7 Vmb6 bVI bIII7 bVIM7 II (R 0 6 1 2 8 6 8 3). In an exact parallel the third chord should be IV7 but he uses IVm7 (with its hidden bVI), emphasizing the minor mode. In the fourth chord the parallel is bIIIM7 but he uses its alternative function Vmb6, the function in which bIII is hidden. The change is subtle. The rest of the progression parallels the first block, including the climactic tritone-removed motion at the end. The effect is even more extraordinary here, as he jumps from the minor region to the supra-major. A more normatively conventional progression would go bVI-7 V. In this passage we see that tritoneremoved relations were already known at the beginning of the 17th century, although their extensive exploitation had to wait until the 19th century. Returning to more conventional territory, here is a passage illustrating the normative use of various dominant substitutes. It comes from Brahms' Sonata for Violin and Piano in A, op. 100. It runs: I VIIo I IIm IIm6 I V17 IIm #lo IIm bIII VIo bVII V7 (R 0 (10) 0 4 4 0 5 4 (14) 4 6 (6) 4 1). The diminished triads VIIo, #lo, and VIo act conventionally as dominant substitutes that ‘stabilize’ some resolution, as in VIo bVI I. The IIm6 acts as a recessive substitute for V7. The VI7 acts as an extended dominant to IIm. The movement from IIm to bIII is more unusual, a type 10 change and a substitute for IIIm by the mixture of modes. The progression shows how important diminished triads are to conventional tonality. Consider this passage from Schumann's Bunte Blatter op. 99/2. It illustrates the normative use of the 7#5 dominant substitute. It goes: I Vaug I IIIm ( VIm6 V117#5 VII7 IIIm ) #1o7 IIm II7 V7 (R 0 1 0 8 6 9 9 8 (14) 4 3 1). The four chords in brackets indicate a digression or brief modulation to the intermediate goal IIIm. With that referent the bracketed progression goes IVm6 V7#5 V7 Im. After this group the #l07 (like VI7) directs the movement back to IIm and on to a conventional conclusion. The 7#5 chord appears for melodic reasons and normatively resolves to its seventh chord cousin. It usually acts in this manner as a dissonant prefix, but in advanced harmony it can also stand alone without its seventh chord base. Early on in the progression the V augmented triad (elements 5 7 #2) is very closely associated with the V7#5 (elements 5 7 #2 4). Augmented triads can be treated as 7#5 subsets. At the ending of Prélude ŕ l 'aprčs-midi d'un faune by Debussy we find an ingenious and unorthodox progression of ‘pedal-point’ chords over the tonic. It falls into two segments: the first part moves from I to bVI, then it pauses and proceeds to IVM7 and on to the final plagal cadence. It goes: I bVlm bVII bVm bVI I7,b2 bVII bVIm IVM7 I (R 0 7 4 11 8 0 4 7 2 0). This unusual progression shows that hopping between regions is not confined to the late 16th century. The initial jump from the major (I) to the flat-minor region (bVIm) rivals anything in Gesualdo. This function is quite complex, since the pedal-point results in a union of bVIm and bVI. Like in the renaissance practice, Debussy fills in the space of the big jump. Here he leaps to the major-minor border function bVII. Then he jumps even further out to the remote bVm function in the flat-minor region, returning to the bVI of the minor region. One can derive this progression by tritone-removed relations from the largely diatonic progression I IIm bVII Im bVI (R 0 4 4 0 8). The second part of the progression is equally brilliant. The I7,b2 hides the IIIo7 diminished tetrad chord that conventionally resolves to IV(m), anticipating the IVM7. But first it unusually resolves into bVII from where the region-hopping commences anew. Again the bVIm could be derived from IIm so that the underlying structure is I7,b2 bVII IIm IVM7 (R 0 4 4 2). Thus the underlying substructure is a diatonic progression of the mixolydian-dorian type. This diatonic base has been transformed by tritone-removed substitutes. The progression is most unusual in its travel to the flat-minor region rather than the more frequented supra-major region. The upcoming Wagnerian excerpt also features the flat-minor region. One more example shows the brilliance of Gesualdo's work. At the beginning of the madrigal Resta di darmi noia he progresses from V to VI. In G, it moves thus: V Im bVI VIm7 V1m6 I III VI (R 1 0 8 6 6 0 7 5). Then he proceeds to make a parallel progression in A. Using the dominant in the initial position rather than the tonic is unusual, although it occasionally occurs already in the 15th century. Gesualdo firmly establishes the minor mode, but then invokes a 14 move (mixing of modes) from bVI to VIm. Thereafter he never goes back to the minor, instead jumping out to the supra-major region. The big leap from I to III is ameliorated by the VI where the pause adds to the feeling of resolution. Then he uses this VI as an unusual pivot: it become V of the key of A, whereupon the same progression is repeated. In this way the two blocks of the progression are inter-locked. The employment of V1m6 is unusual. Normatively it resolves to IIIm or to V rather than I. Had he used VIm the relation would be close, but the appearance of V1m6 instead illustrates an early historical instance where a seventh chord is employed more for local color than for conventional function. Finally, I want to look at a passage that illustrates the normative use of the 7b5 chord and the importance of the power positions. I can do no better than the beginning of the Prelude to Wagner's Tristan and Isolde. In order to emphasize the fact that this brilliant music is perfectly playable in 31-et, I will indicate a septimal chord where appropriate. In Am, the first chord block goes: VIIm+6 II7b5 V7b5 V7 (R 10 3 1 1). Note that every function forms part of my table of dominant substitutes. The septimal form VIIm+b is appropriate because it points to the V7 goal, and also because the introductory melody goes 1 b6 5 #4. With the scalar elements b6 and #4 we enter the territory. The composer now shifts the pattern up a minor third and slightly modifies the progression: IIm6 VII7b5 bVII7b5 bVII7 (R 4 9 4 4). The VII7b5 can be derived from IV-7#4 but, again, all of the functions form part of the set of significant dominant substitutes. Having transposed the pattern up a minor third one would expect him to do it again and put the pattern on IVm. Wagner uses such diminished chord-based sequences quite often. However, here he skips over the IVm position and instead jumps up yet another minor third to bVIm, a tritone from IIm. Now the progression is slightly expanded and goes: bVIm6 bVIm7 bIIIaug II7b5 II7 (R 7 7 6 3 3). Having shifted progressively far into the flat-minor region he has created considerable tension to resolve on the dominant. He magnifies this stress by repeating the chord block. The bVIm6 naturally resolves to bIII but instead he uses bIIIaug (like bIII7#5) anticipating his move to the dominant. The final chord block of the passage resolves the whole thing on the dominant, but instead of ending on the usual tonic he pauses on bVI. If we ignore the various linear complexities it goes: V7 IIm Vm7 V7 bVI (R 1 4 2 1 8). Note that the passage as a whole has used mostly functions from the table of dominant substitutes. Even the section from bVIm6 to II7 can perhaps be functionally enhanced by using the alternative version #Vm+6 #Vm7 Vaug II7b5 II7 (R 16 16 1 3 3). In this case even more of the passage derives from the table. I should point out though, that Wagner is not likely to have had any awareness of function 16. The function 7 was certainly his intention, Moreover, the use of 16 instead of 7 results in a slight change in the lineup of chords (another variant of the augmented triad) as well as some alteration in the buildup of stress in the passage. It doesn't alter its goal orientation. The historical progressions of my sample make visits to the supra-region or more rarely to the flat-minor region. They usually don't visit them together in one progression. However, this structure is entirely possible. Take, for example, this progression showing the following trait: with every change of chord it shifts its region. It goes: I bIIm bVIIm IIIm VI IIm IVm6 I (R 0 9 3 8 5 4 1 0). The progression highlights the rank 11 tritone-shift change of bVIIm to IIIm, but the only unusual movement here is the 9 type change from I to bIIm. This rank displays E13 with its attendant enharmonic shifthere from 3 to b4. The rest of the progression uses common changes found in classical progressions. This example shows that access to wider regions are possible even when we restrict ourselves mostly to traditional movements. By the way, the complimentary progression by reciprocity is perhaps even more attractive, since it uses mostly major chords and ends with the assertive dominant. It goes: Im VII II bVI bIIIm bVII V7 Im (R 0 9 3 8 5 4 1 0). Here the initial movement entails an enharmonic shift between b3 and #2. Traditional harmony tolerates some wide jumps, as long as they mostly occur between the major and minor regions. A good example can be found in the 14 change used in the mixing of modes. But we can also employ these same means to propel ourselves to a remote function. Take this movement: I VIm VI #Vlm (R 0 6 5 20). Now we sit in the distant sharp-major region in the middle of the septimal zone. One may rightly ask whether such a movement is permissible. Does it not destroy the fabric of tonality? In my opinion it does not, as long as it is eventually directed back toward the tonic. For example, the movement may continue: #VIm #I #IVm VI IIm IVm6 I (R 20 13 12 5 4 1 0). Alternatively we could short-cut the process with a type 14 change by going #VIm #I #IVm IV. I have used the E9 shift 14 as an example, but of course any member of the little table will do. However, each one will ‘do’ in its own manner. As we have seen from the historical examples, the most notorious and theoretically fraught movement is the E11 tritone shift of rank 12 in the major and 12 in the minor. It explains much of what occurs in advanced chromatic progressions. The remote function #VIm above can also be reached as a 12 movement from IIIm. Chromatic harmony comes mostly from the interpolation of such movements into diatonic harmony. For example, take the Ionian major normative sequence IIIm VIm IIm V7 (R 8 6 4 1). By inserting substitutions it becomes #VIm VIm #Vm V7 (R 20 6 16 1) or alternatively IIIm #IIm IIm bII-7 (R 8 18 4 10). Take the reciprocal normative sequence in the aeolian minor mode bVI bIII bVII lVm6 (R 8 6 4 1). It becomes bbIII bIll bIV IVm6 (R 20 6 16 1) or alternatively bVI bbVII bVII VIIm+6 (R 8 18 4 10). The musician accustomed to 12-et will ask why we don't replace bbIII, bbVII, and bIV (R 20, 18, and 16) with the more familiar II, VI, and III (R 3, 5, and 7). Of course, we may do so, but then we have interpolated alternative movements with a different dynamic. 12-et confuses these functions while 31-et preserves their identity. This method of interpolating transpositions into some normative sequence can be generalized to any rank number and any sequence. Many interesting progressions can be generated by this approach, progressions that wander to distant places and yet find their way home. Interesting progressions also emerge from the imposition of sequences, the method we saw in Josquin and Brahms. In this example of such a progression we go right around the 31-et circle in short order. It goes: Im bI bIVm xll xVm #V #Im I (R 0 14 15 30 30 15 14 0). This progression uses a sequence of alternating 14 and 1 movements that divide the circle roughly into quarters, represented by ranks 30 and 30 at the antipodes and ranks 14 and 15 about half-way. Such a progression is simply impossible in 12-et or even in 19-et. It illustrates an instance of advanced antipodal harmony in 31-et. One can argue whether or not this progression is tonal at all. It can be interpreted either way but in any case it is peculiar to the 31-et system. A whole variety of such unusual progressions are perfectly feasible using various sequences. The practicality of a distant jump involves how many elements they have in common. For example, take this progression: Im II VIIm bII bVIIm I (R 0 3 10 10 3 0). The wide jump from VIIm to bII is slightly awkward since they have no elements in common. However, when we thicken them into VIIm+6 and bII-7 they now have two elements in common (b6 and 7). Consequently, the transition becomes much smoother. It could become yet more fluid if we interpolate VIIo7 between them. In a similar manner, the transition from Im to II can be smoothed over by interpolating Im6,#4. We can apply such procedures to any awkward jump. As an extreme example, take the remote power positions #Vm+6 and bIV-7. They have an antipodal relation to each other with no elements in common. This difficult transition can be aided by again interpolating VIIo7. Now they have some elements in common, although we still cannot avoid enharmonic shifts. Alternatively we could interpolate V7#5 and bII-7#4. Using these transitional dominant substitutes we have spanned an extreme distance. The Reciprocity Model is admittedly quite abstract. It says nothing about rhythm, voice leading, figuration, and the overall distribution of chords-factors that greatly influence the movement of progressions. Instead of specific voicings the model employs only the more abstract unordered sets. It also restricts itself to the most basic of chord types. In spite of these limitations something of value emerges. The model makes visible the norms that underlie chord progressions within tonal harmony. Of course, norms are not rules. As we have seen in the historical examples, norms can be followed, thereby fulfilling expectations. But they can also be flouted, creating surprise or novel effects. The most effective chord progressions take advantage of these expectations by placing the `errant' element in the most strategic position by rhythm and voicing. Siemen Terpstra, Amsterdam, January 2011
|