
|
Over zuivere intonatie. Het levenswerk van prof. dr. A. D. FokkerAan prof. dr. A. D. Fokker, die in augustus 1967 de 80-jarige leeftijd bereikte, komt de grote verdienste toe de inzichten van figuren als Zarlino, Vicentino, Christiaan Huygens en Leonhard Euler te hebben uitgewerkt en gebundeld. Fokkers ideeën omtrent zuivere intonatie, die hun neerslag vonden in de 31-toonstemming, leidden ertoe dat in 1950 door de firma B. Pels en Zoon (Alkmaar) een 31-toonorgel gebouwd werd, dat geplaatst werd in het Teylermuseum te Haarlem. Daar vinden op de eerste zondag van de maand (uitgezonderd in januari en februari) bespelingen plaats, die georganiseerd worden door de Stichting Huygens-Fokker, welke een voortzetting is van de in 1960 opgerichte Stichting Nauwluisterendheid. De Stichting Huygens-Fokker (secretariaat: Zieseniskade 7 III te Amsterdam) stelt zich ten doel, begrip te wekken voor de grotere zuiverheid, welke met het toepassen van de 31-toonstemming (een stemming met zuivere tertsen en zuivere, natuurlijke septiemen) wordt bereikt. De belangstelling voor de 31-toonstemming neemt voortdurend toe, ook in het buitenland, maar vaak blijkt de gedachtengang, welke eraan ten grondslag ligt vele musici en muziekgeïnteresseerden nog vreemd te zijn. Wij menen er goed aan te doen, deze gedachtengang, welke heus niet ontoegankelijk behoeft te zijn (en die in de muziekpraktijk van grote betekenis kan zijn en verhelderend kan werken), eens in kort bestek uiteen te zetten.
Het menselijk oor ervaart een interval als "zuiver" wanneer er geen zwevingen
te horen zijn. De natuurkunde leert ons dat zulk een zwevingvrij interval
bestaat uit twee tonen waarvan de trillingsgetallen aan een eenvoudige
getalsverhouding beantwoorden. Bij een zuiver oktaaf is deze getalsverhouding
1:2, bij een zuivere kwint 2:3, bij een zuivere kwart 3:4, bij een zuivere
grote terts 4:5, bij een zuivere kleine terts 5:6, bij een zuivere grote sext
3:5, bij een zuivere kleine sext 5:8, etcetera. Alle tonen waarmee deze
intervallen kunnen worden gemaakt kunnen door bespelers van strijkinstrumenten
eenvoudig ten gehore worden gebracht, namelijk als natuurlijke
flageolettonen.
De laagst genoteerde toon is de grondtoon of eerste harmonische; de andere
tonen (vaak boventonen genoemd) zijn de tweede, de derde harmonischen
etcetera, Deze harmonischen kunnen (misschien met uitzondering van de laagste)
ook door bespelers van koperen blaasinstrumenten worden weergegeven. Ook
intervallen die in onze westerse muziek niet worden erkend, zoals die waarbij
de zevende of de elfde harmonische zijn betrokken, klinken ons
zuiver in de oren, omdat ook hierbij geen zwevingen te horen zijn. Wij noemen
in dit verband de infraterts (6:7), de supraseconde (7:8),
en de harmonische septiem (4:7).
Uitgaande van bijvoorbeeld de losse c-snaar van de altviool kunnen wij op
verschillende manieren een e-tweegestreept (losse e-snaar der viool) bereiken:
a. door opeenstapeling van vier kwinten:
(Dit zijn dus de tonen, geproduceerd door de losse snaren van alt en viool);
b. door de vijfde harmonische van de c-snaar der altviool te spelen:
De beide bereikte e's nu zijn niet gelijk van toonhoogte; het interval tussen
losse c-snaar en losse e"-snaar doet ons oor onaangenaam aan: de e"-snaar komt
ons te hoog voor. De vijfde harmonische van de c-snaar is lager. Een kleine berekening leert ons dat de losse e"-snaar een trillingsgetal heeft van 3/2 × 3/2 × 3/2 × 3/2 = 81/16 maal het trillingsgetal van de c-snaar; de vijfde harmonische van de c-snaar heeft echter een trillingsgetal van 5 (= 80/16) maal het trillingsgetal van de c-snaar.
Het verschil in toonhoogte tussen de beide e"'s (uitgedrukt door de verhouding
80/81 der trillingsgetallen) is het zogenaamde syntonische komma. In de
praktijk van het musiceren ontmoet men met dit komma moeilijkheden.
Wij zagen in het bovenstaande reeds, dat op strijkinstrumenten die in zuivere
kwinten zijn gestemd, de losse c- en e-snaren geen zuiver interval vormen.
Ieder strijkkwartet zal dit gemakkelijk kunnen constateren. Maar ook op een in
zuivere kwinten gestemde viool bijvoorbeeld is het akkoord: Wat gebeurt er nu wanneer wij in plaats van zuivere kwinten, bijvoorbeeld zuivere grote tertsen opéén gaan stapelen? Indien men drie grote tertsen op elkaar stapelt, ontmoet men een ander zeer klein interval. Op twee violen is dit eenvoudig te demonstreren, als volgt:
 Bij bovenstaande proe£ stellen wij (waarschijnlijk tot veler verbazing) vast dat, uitgaande van zuivere (zwevingvrije) grote tertsen, er een zeer duidelijk toonhoogteverschil bestaat tussen bes en ais of, algemener gezegd: tussen al die tweetallen van tonen die gewoonlijk enharmonisch verwisselbaar genoemd worden, met dien verstande dat de bes hoger ligt dan de ais, de des hoger dan cis, enz. Iedere terts betekent een trillingsgetalsverhouding 4:5. In bovenstaand voorbeeld heeft dus de bereikte ais' een trillingsgetal van 5/4 × 5/4 × 5/4 = 125/64 maal het trillingsgetal van de bes waarvan wij uitgingen. De bes' echter (de laatste noot in de eerste viool) heeft een trillingsgetal van 2 (= 128/64) maal dat van de bes waarvan wij uitgingen. Het intervalletje ais' - bes' beantwoordt dus aan de trillingsgetalsverhouding 125:128. Het interval tussen bes en ais blijkt groter te zijn dan het komma, en wel bijna tweemaal zo groot. Het wordt de kleine diëze genoemd. Ook bij de opeenstapeling van vier zuivere kleine tertsen vinden we een soortgelijk toonhoogteverschil tussen twee zogenaamde enharmonisch verwisselbare tonen; weer is bes hoger dan ais enz.
De meeste musici zijn van mening dat een bes lager moet klinken dan een
ais. Niettemin hebben wij hierboven gezien dat onomstotelijk, gerekend naar
zuivere grote tertsen, die mening op een dwaling berust. Hun dwaling is
deze, dat in plaats van met consonante zuivere tertsen te werken, zij met te
grote dissonante, zogenaamde Pythagoras-tertsen rekenen. Deze zijn een komma
groter.
bes ---------- d' ---------- fis' ---------- ais' - bes'
(10 diëzes) (10 diëzes) (10 diëzes) (1 diëze)
Om zoals bij normaal gestemde klavierinstrumenten het verschil in toonhoogte
tussen bes en ais weg te moffelen moet men (dat volgt uit het bovenstaande)
de drie grote tertsen bes-d, d-fis en fis-ais elk één derde deel van een
diëze te groot stemmen, dat is 3,6% van een grote terts. Voor geoefende oren is
duidelijk te horen dat inderdaad op de klavierinstrumenten alle grote tertsen te
groot zijn. In de 31-toonstemming is dit niet het geval: de grote tertsen klinken
hierin prachtig zuiver. In Sir James Jeans' Science and Music (Ned. vert. dr. E.J. Dijksterhuis) lezen wij (pag. 166) dat de aanvaarding van de gelijkzwevende stemming (beter gezegd: de evenredige stemming) slechts heel langzaam kwam vooral in Engeland; pas in het midden der 19de eeuw begon men de Engelse piano's volgens het nieuwe systeem te stemmen, en bij geen van de Engelse orgels op de grote tentoonstelling van 1851 was het toegepast. De reden waarom op den duur de middentoonstemming toch is verdrongen door de evenredige stemming is dan ook uitsluitend gelegen in het feit dat men in de middentoonstemming niet onbeperkt kan moduleren en niet in alle toonsoorten kan spelen. De 31-toonstemming is op te vatten als een "uitgebouwde" middentoonstemming met toetsen voor cis én voor des, voor gis én voor as, enz., en combineert dus de voordelen van welluidendheid en onbeperkte mogelijkheid tot moduleren. Het is interessant te weten dat reeds in de 16de eeuw de componist Nicola Vicentino (1511-1572?), leerling van Adr. Willaert, trachtte een zogenaamd archicembalo te vervaardigen met 31 toetsen per oktaaf! Van groot belang is deze middentoonstemming speciaal bij strijkinstrumenten. Men stemt daarbij het instrument zó, dat alle kwinten gevormd door de losse snaren een tikje kleiner zijn, haast onmerkbaar voor het oor. (Bij de in kwarten gestemde contrabas moeten de kwarten juist een tikje groter worden gemaakt.) Het Hongaars Strijkkwartet doet dit, en iets dergelijks wordt vermeld van Pablo Casals (R. von Tobel, P.C.). Intonatiemoeilijkheden zoals in de notenvoorbeelden 2, 3 en 4 van dit artikel zijn door deze manier van stemmen opgelost. De notatie en benaming der noten in de 31-toonstemming is als volgt: Een grote terts (10 diëzes) wordt verdeeld in twee grote secondes, elk van 5 diëzes:  De eerste maal, dat de verdeling van de grote seconde in vijf stappen wordt aanbevolen, vinden wij reeds in de verhandelingen van Marchettus van Padua (begin 14de eeuw), een muziek-theoreticus ten tijde der Ars Nova! De vijf stappen van c naar d worden als volgt genoteerd met half kruis, kruis, anderhalf kruis en dubbelkruis: 
De genoteerde noten worden respectievelijk genoemd: c - ci - cis - cisi -
cisis - d. 
Deze noten worden respectievelijk genoemd: d - dèh - des - desèh - deses - c.
De volgende notenparen uit bovenstaande voorbeelden zijn identiek: ci = deses;
cis = desèh; cisi = des; cisis = dèh.  De namen van bovenstaande noten zijn: b - bi - bis - c; en c - cèh - ces - b. Identiek zijn: bi = ces; bis = cèh.
Bij de 31-deling van het oktaaf kunnen bijna alle ons bekende intervallen
aanmerkelijk zuiverder worden getroffen dan bij de 12-deling. Er wordt verschil
gemaakt tussen grote en kleine halve tonen (diatonische, respectievelijk
chromatische halve tonen, 3 respectievelijk 2 diëzes groot). Componisten die
zich met de 31-toonschaal bezighouden moeten zich dus terdege rekenschap
geven of ze cis of des, gis of as, enz. bedoelen, en dit goed noteren, want het
toonhoogteverschil tussen deze noten komt hier tot zijn recht.
Voor componisten die de moeite nemen zich in deze materie te verdiepen,
liggen in de 31-toonstemming een overstelpende hoeveelheid mogelijkheden.
Deze stemming biedt bijvoorbeeld de mogelijkheid exotische intervallen (en
dus ook exotische melodieën en harmonieën) weer te geven, zoals die welke
worden toegepast bij de verschillende soorten van gamelan (namelijk de
supraseconde 7:8, 6 diëzes groot), de doedelzakmuziek (het interval 10:11,
iets kleiner dan onze grote seconde, 4 diëzes groot), de Arabische
muziek (met de zogenaamde midgrote terts, dat is een interval juist tussen grote en
kleine terts gelegen, 9 diëzes groot), enz. enz. - Inderdaad vele mogelijkheden om aan
het 12-toonkeurslijf te ontsnappen! Literatuur
Henk Badings schreef tweemaal een
Preludium en Fuga, alsmede een reeks kleine
stukken voor het 31-toonorgel. Voorts componeerde hij in de 31-toonstemming
driemaal een Sonate voor twee violen en een a-cappella-koor
Contrasten.
Anton de Beer ontwierp een tweedelige Methode
voor 31-toonklavier, alsmede een Sonate, een Sonatine en
enige Kleine speelstukken.
Jan van Dijk schreef
tweemaal een Musica voor 31-toonorgel, twee a-cappella-koren
(Deuntje en Hymne), een Concerto voor trombone, viool en
violoncel, Vier harmonisch,
melodische Intonatie-oefeningen voor strijkkwartet en Vierstemmige
intonatie-oefeningen voor gemengd koor a cappella.
Jaap Geraedts schreef Zes Studies in Eulers toongeslachten voor fluit
en voor twee fluiten.
Anthon van der Horst componeerde een
Suite voor 31-toonorgel.
Professor Fokker vervaardigde zelf onder het pseudoniem Arie de Klein onder
meer Zes Bagatellen op tien toetsen, Kalenderblaadjes in de kringloop
van acht, een Passacaglia, Kringspiegelingen en In
generibus Leonhardi Euleri.
Hans Kox schreef Drie stukken voor vioolsolo,
Vues des Anges voor viool en bariton, Vier stukken voor
strijkkwartet, een Passacaglia en Koraal voor 31-toonorgel en
Vier didactische stukken voor twee trompetten en trombone.
Bouw Lemkes stelde Intonatie-oefeningen samen voor twee violen in de 31-toonstemming.
Peter Schat schreef een Collage voor
31-toonorgel. Naast deze Nederlandse bijdragen zijn er nog composities van
Eugen Frischknecht, Joel Mandelbaum,
Alan Ridout en
Ivan Wyschnegradsky. Bouw Lemkes, 1968
|
Zuivere intonatie |









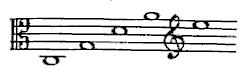


 onmogelijk zuiver te spelen: óf de sekst en de kwint worden zuiver gespeeld
(dan is de kwart een komma te groot) óf men maakt die kwart en de kwint
daaronder zuiver, en dan wordt de sekst een komma te groot. Een soortgelijk
verschijnsel ontmoeten wij bij het spelen van:
onmogelijk zuiver te spelen: óf de sekst en de kwint worden zuiver gespeeld
(dan is de kwart een komma te groot) óf men maakt die kwart en de kwint
daaronder zuiver, en dan wordt de sekst een komma te groot. Een soortgelijk
verschijnsel ontmoeten wij bij het spelen van: